What Is The Gcf Of 8 And 52
Treneri
May 14, 2025 · 6 min read
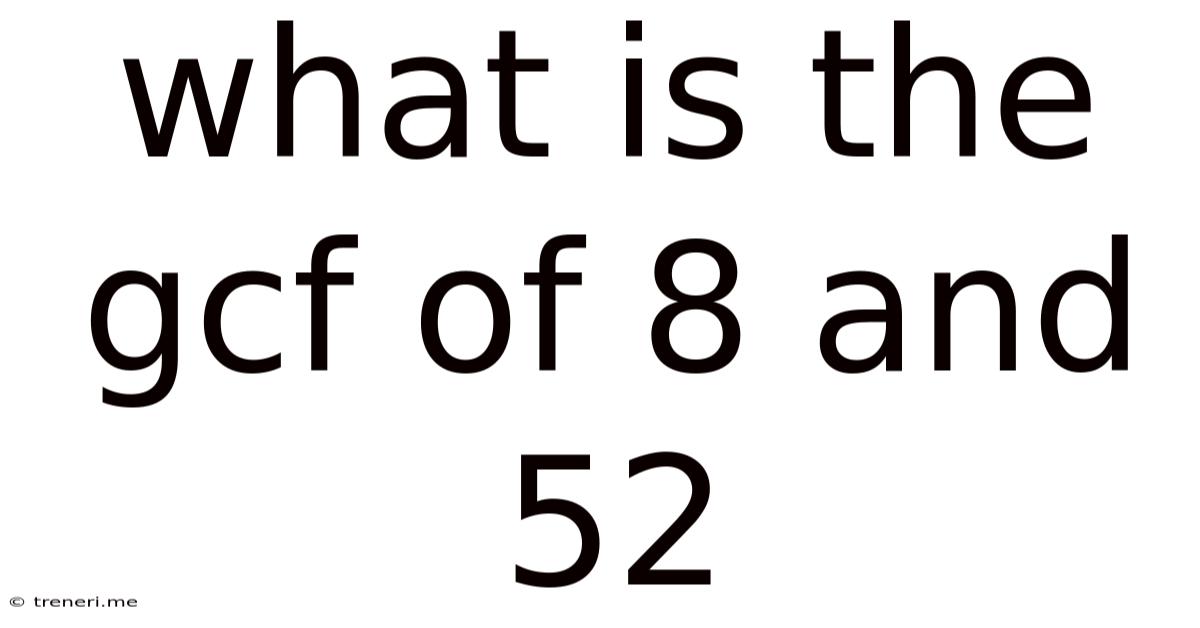
Table of Contents
What is the GCF of 8 and 52? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers is a fundamental concept in mathematics, crucial for simplifying fractions, solving algebraic equations, and understanding number theory. This article will explore how to find the GCF of 8 and 52, detailing various methods and explaining the underlying principles. We’ll go beyond simply finding the answer and delve into the practical applications and theoretical underpinnings of this essential mathematical operation.
Understanding the Greatest Common Factor (GCF)
Before we tackle the specific problem of finding the GCF of 8 and 52, let's establish a solid understanding of what the GCF actually represents. The greatest common factor, also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the two or more numbers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
For example, consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
The simplest method for finding the GCF, especially for smaller numbers, is to list all the factors of each number and then identify the largest factor common to both. Let's apply this method to find the GCF of 8 and 52:
Factors of 8:
1, 2, 4, 8
Factors of 52:
1, 2, 4, 13, 26, 52
Common Factors:
Comparing the two lists, we can see that the common factors of 8 and 52 are 1, 2, and 4.
Greatest Common Factor:
The largest common factor is 4. Therefore, the GCF of 8 and 52 is 4.
This method is straightforward and easy to understand, making it ideal for introductory lessons on GCF. However, for larger numbers, this method becomes increasingly cumbersome and time-consuming.
Method 2: Prime Factorization
A more efficient method, particularly for larger numbers, is to use prime factorization. Prime factorization involves expressing a number as the product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Let's apply this method to find the GCF of 8 and 52:
Prime Factorization of 8:
8 = 2 x 2 x 2 = 2³
Prime Factorization of 52:
52 = 2 x 2 x 13 = 2² x 13
Identifying Common Prime Factors:
Now, we identify the common prime factors in both factorizations. Both 8 and 52 share two factors of 2 (2²).
Calculating the GCF:
To find the GCF, we multiply the common prime factors together: 2 x 2 = 4. Therefore, the GCF of 8 and 52 is 4.
This method is more efficient than listing factors, especially when dealing with larger numbers. The prime factorization provides a structured approach, making it less prone to errors.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean Algorithm to find the GCF of 8 and 52:
-
Start with the larger number (52) and the smaller number (8).
-
Divide the larger number by the smaller number and find the remainder.
52 ÷ 8 = 6 with a remainder of 4.
-
Replace the larger number with the smaller number (8) and the smaller number with the remainder (4).
-
Repeat step 2.
8 ÷ 4 = 2 with a remainder of 0.
-
Since the remainder is 0, the GCF is the last non-zero remainder, which is 4.
Therefore, the GCF of 8 and 52 is 4.
The Euclidean Algorithm is computationally efficient and is widely used in computer science and cryptography for its speed and accuracy in finding the GCF of very large numbers.
Applications of Finding the GCF
The ability to find the greatest common factor is not merely an academic exercise; it has practical applications across various mathematical fields and real-world scenarios. Here are some examples:
-
Simplifying Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For example, the fraction 52/8 can be simplified by dividing both the numerator and the denominator by their GCF (4), resulting in the simplified fraction 13/2.
-
Solving Algebraic Equations: The GCF plays a crucial role in factoring algebraic expressions. Factoring allows us to solve quadratic equations and other polynomial expressions more easily.
-
Number Theory: GCF is a cornerstone concept in number theory, used in various theorems and proofs related to divisibility and prime numbers.
-
Real-world Applications: GCF finds application in various practical scenarios, such as dividing objects into equal groups, determining the size of the largest square tile that can cover a rectangular floor without any cuts, and more.
Beyond the Basics: Exploring Further Concepts
The concept of GCF expands beyond just two numbers. We can also find the GCF of three or more numbers using the same methods discussed above. For instance, to find the GCF of 8, 52, and 24, we would apply prime factorization or the Euclidean Algorithm to the set of numbers.
Furthermore, the concept is intimately linked to the least common multiple (LCM). The LCM is the smallest positive integer that is divisible by all the numbers in a set. There's a relationship between the GCF and LCM of two numbers (a and b):
GCF(a, b) * LCM(a, b) = a * b
This relationship provides a shortcut to calculate the LCM if the GCF is already known, and vice versa.
Conclusion: Mastering the GCF
Finding the greatest common factor of 8 and 52, as demonstrated through different methods, is a foundational skill in mathematics. Understanding the various approaches – listing factors, prime factorization, and the Euclidean Algorithm – equips you with the tools to tackle this task efficiently, regardless of the size of the numbers involved. Furthermore, recognizing the wider applications of the GCF across diverse mathematical areas highlights its importance in solving practical problems and delving deeper into the fascinating world of numbers. Mastering the GCF is a key step towards a deeper understanding of mathematics and its diverse applications.
Latest Posts
Latest Posts
-
Cuanto Falta Para El 5 De Noviembre
May 15, 2025
-
Conversion De Grados Centigrados A Farenheit
May 15, 2025
-
Cuantos Dias Trae Este Mes De Septiembre
May 15, 2025
-
Cuantos Dias Faltan Para El 14 De Diciembre
May 15, 2025
-
How Much Days Is 200 Hours
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 8 And 52 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.