What Is The Gcf Of 9 And 16
Treneri
May 13, 2025 · 5 min read
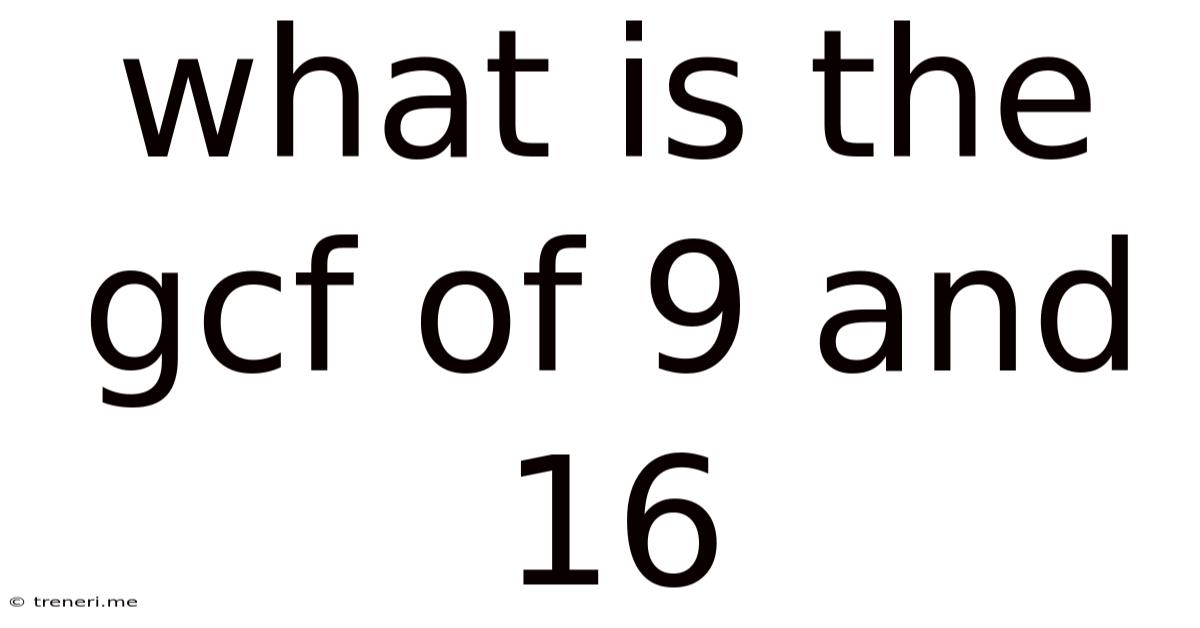
Table of Contents
What is the GCF of 9 and 16? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts and different methods for solving it opens doors to more advanced mathematical concepts. This article will comprehensively explore how to find the GCF of 9 and 16, and then delve into the broader significance of GCFs in various mathematical applications.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's a fundamental concept in number theory with practical applications in various fields, from simplifying fractions to solving complex algebraic equations.
When dealing with smaller numbers like 9 and 16, finding the GCF might seem straightforward. However, understanding the process is crucial for tackling larger numbers and more complex problems.
Methods for Finding the GCF of 9 and 16
Several methods can be employed to determine the GCF of 9 and 16. Let's explore the most common ones:
1. Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor they have in common.
- Factors of 9: 1, 3, 9
- Factors of 16: 1, 2, 4, 8, 16
Comparing the lists, we see that the only common factor is 1. Therefore, the GCF of 9 and 16 is 1.
2. Prime Factorization
Prime factorization involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
Since there are no common prime factors between 9 and 16, their GCF is 1.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 9 and 16:
- 16 - 9 = 7
- 9 - 7 = 2
- 7 - 2 - 2 = 5
- 5 -2 = 3
- 3-2 = 1
- 2 - 1 = 1
The process continues until we reach 1. Therefore, the GCF of 9 and 16 is 1. While this method is effective, it's less intuitive than the previous methods for smaller numbers.
Significance of GCF: Beyond Simple Arithmetic
The concept of GCF extends far beyond simply finding the largest common divisor of two numbers. It plays a crucial role in various mathematical areas:
1. Simplifying Fractions
The GCF is fundamental to simplifying fractions. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, if we have the fraction 12/18, the GCF of 12 and 18 is 6. Dividing both the numerator and denominator by 6 simplifies the fraction to 2/3.
2. Solving Diophantine Equations
Diophantine equations are algebraic equations where only integer solutions are sought. The GCF plays a crucial role in determining whether a Diophantine equation has a solution and in finding those solutions.
3. Modular Arithmetic and Cryptography
Modular arithmetic, where numbers "wrap around" upon reaching a certain value (the modulus), is extensively used in cryptography. The GCF, particularly the extended Euclidean algorithm, is crucial for computing modular inverses, which are essential for many cryptographic algorithms like RSA.
4. Least Common Multiple (LCM) Calculations
The GCF and the least common multiple (LCM) are closely related. The LCM is the smallest number that is a multiple of two or more given numbers. There's a simple formula connecting the GCF and LCM:
LCM(a, b) = (a x b) / GCF(a, b)
Knowing the GCF allows us to efficiently calculate the LCM, which is essential in various applications, such as finding the least common denominator when adding fractions.
5. Abstract Algebra
The concept of GCF extends to abstract algebra, where it's generalized to the concept of the greatest common divisor in rings and other algebraic structures. This generalization is crucial for understanding the structure and properties of these abstract algebraic objects.
Practical Applications of GCF
The applications of GCF are far-reaching and extend beyond pure mathematics:
-
Measurement and Cutting: Imagine you have two pieces of wood, one 9 inches long and the other 16 inches long. If you want to cut both pieces into identical smaller pieces of the largest possible size, the GCF (which is 1 in this case) dictates that the largest identical pieces would be 1 inch long.
-
Resource Allocation: Imagine distributing 9 apples and 16 oranges equally among several people. Since the GCF of 9 and 16 is 1, you can only distribute them one item at a time per person.
-
Scheduling and Timing: GCF can be used to determine the timing of events that occur periodically. For example, if two machines complete cycles in 9 and 16 hours respectively, the GCF helps determine when they'll both complete a cycle simultaneously.
-
Computer Science: GCF algorithms are implemented in computer programs for various tasks, including simplification of fractions, cryptographic applications, and optimization problems.
Conclusion: The Unsung Hero of Number Theory
While seemingly simple at first glance, the GCF of 9 and 16 (which is 1) represents a fundamental concept in number theory with profound implications in various mathematical fields and practical applications. Understanding the different methods for finding the GCF, as well as its significance in simplifying fractions, solving equations, and more, provides a solid foundation for further exploration of advanced mathematical topics. The seemingly simple question of "What is the GCF of 9 and 16?" opens a door to a world of mathematical exploration and practical problem-solving. The power of GCF lies not just in its calculation but in its widespread utility across numerous disciplines.
Latest Posts
Latest Posts
-
411 Rounded To The Nearest Hundred
May 13, 2025
-
What Size Mirror For A 24 Inch Vanity
May 13, 2025
-
Does Two Quarts Equal A Gallon
May 13, 2025
-
How Many Oz Is 1 5 Pounds
May 13, 2025
-
Which Side Lengths Represent The Sides Of A Right Triangle
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 9 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.