What Is The Gcf Of 9 And 18
Treneri
May 14, 2025 · 5 min read
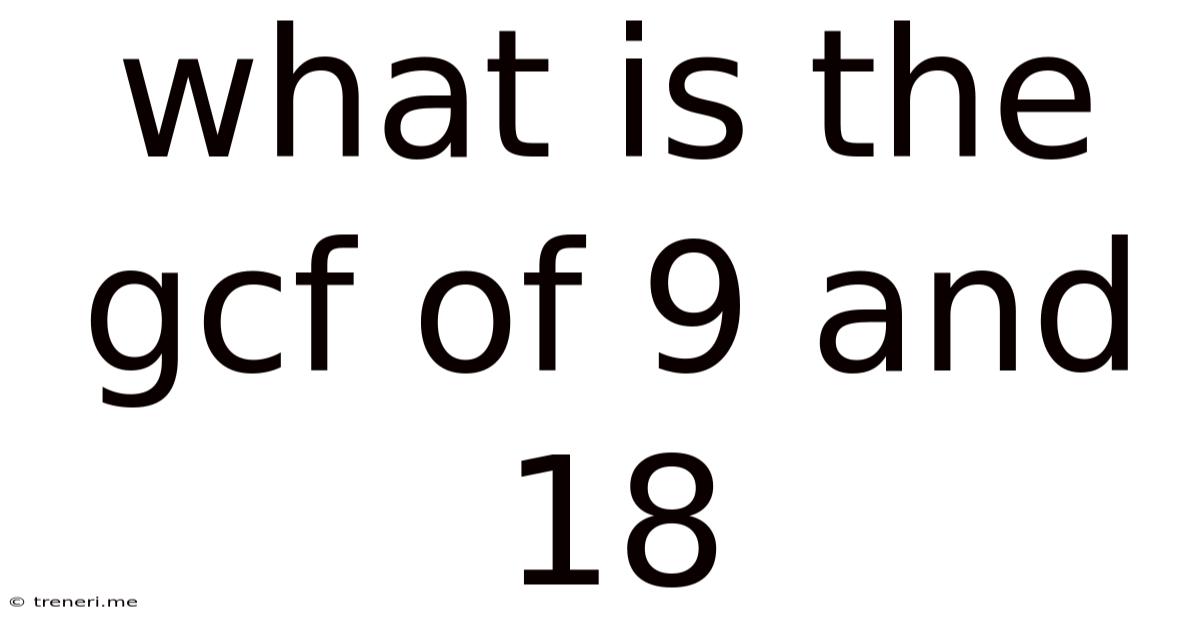
Table of Contents
What is the GCF of 9 and 18? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can significantly enhance your mathematical skills. This comprehensive guide will delve into the question, "What is the GCF of 9 and 18?", providing multiple approaches to solve this problem and expanding on the broader significance of GCFs in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific problem of finding the GCF of 9 and 18, let's establish a clear understanding of what a GCF is. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
Why are GCFs Important?
GCFs are fundamental in various mathematical operations and real-world applications. They're crucial for:
- Simplifying Fractions: Finding the GCF allows you to reduce fractions to their simplest form. For instance, the fraction 18/9 can be simplified using the GCF.
- Solving Algebraic Equations: GCFs play a significant role in factoring polynomials, a crucial step in solving many algebraic equations.
- Geometry and Measurement: GCFs are used in determining the dimensions of objects with specific constraints, like finding the largest square tile that can perfectly cover a rectangular floor.
- Real-World Problem Solving: Many practical problems, from dividing items equally to arranging objects in arrays, involve finding the GCF to optimize solutions.
Methods for Finding the GCF of 9 and 18
Several effective methods can be used to determine the GCF of 9 and 18. Let's explore the most common and practical ones:
1. Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both.
- Factors of 9: 1, 3, 9
- Factors of 18: 1, 2, 3, 6, 9, 18
By comparing the two lists, we can see that the common factors are 1, 3, and 9. The greatest of these common factors is 9. Therefore, the GCF of 9 and 18 is 9.
2. Prime Factorization
This method utilizes the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime Factorization of 9: 3 x 3 = 3²
- Prime Factorization of 18: 2 x 3 x 3 = 2 x 3²
To find the GCF using prime factorization, identify the common prime factors and their lowest powers. Both 9 and 18 share two factors of 3 (3²). Therefore, the GCF is 3 x 3 = 9.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which represents the GCF.
Let's apply the Euclidean algorithm to 9 and 18:
- 18 - 9 = 9 (Replace 18 with 9)
- Now we have 9 and 9. Since the numbers are equal, the GCF is 9.
Expanding on the Concept of GCF
The concept of GCF extends beyond finding the GCF of just two numbers. You can also find the GCF of three or more numbers using similar methods. For multiple numbers, you would find the prime factorization of each number and identify the common prime factors with their lowest powers. Alternatively, you can use the Euclidean algorithm iteratively.
Real-World Applications of GCF
Let's explore some real-world scenarios where understanding GCFs proves invaluable:
1. Dividing Treats Equally
Imagine you have 18 cookies and 9 candies. You want to divide them equally among your friends without having any leftovers. The GCF will tell you the maximum number of friends you can have. The GCF of 18 and 9 is 9, meaning you can divide the treats equally among 9 friends.
2. Arranging Objects in Arrays
Suppose you're arranging 18 square tiles to form a rectangle. To maximize the area and create a visually pleasing arrangement, you'd look for the factors of 18. Using the factors, you could create rectangles of various dimensions (1x18, 2x9, 3x6, 6x3, 9x2, 18x1). If you had 9 tiles, your possibilities would be limited to (1x9, 3x3, 9x1).
3. Simplifying Fractions
Let's say you have the fraction 18/9. To simplify this fraction, find the GCF of 18 and 9, which is 9. Divide both the numerator and denominator by 9, resulting in the simplified fraction 2/1 or simply 2.
4. Measurement and Geometry
Imagine you need to cut a 18-inch long ribbon and a 9-inch long ribbon into pieces of equal length, maximizing the length of each piece. The GCF of 18 and 9 (which is 9) determines the largest possible length of the pieces without any waste.
Conclusion: Mastering GCFs
Understanding the greatest common factor (GCF) is essential for a solid foundation in mathematics. From simplifying fractions and solving algebraic equations to practical applications in everyday life, the GCF provides a powerful tool for problem-solving. By mastering the methods outlined in this guide, from listing factors and prime factorization to the efficient Euclidean algorithm, you can confidently tackle various problems involving GCFs and appreciate their broader mathematical significance. Remember, the GCF of 9 and 18 is 9, a fact you can now derive using multiple approaches. Continue practicing these methods to build fluency and strengthen your mathematical intuition.
Latest Posts
Latest Posts
-
How Can I Calculate My Electricity Bill
May 15, 2025
-
Cuantos Dias Pasaron Desde El 4 De Mayo Hasta Hoy
May 15, 2025
-
How Many Days Is 2000 Minutes
May 15, 2025
-
Cuanto Es 54 Fahrenheit En Centigrados
May 15, 2025
-
1 3 Squared As A Fraction
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 9 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.