What Is The Greatest Common Factor For 12 And 54
Treneri
May 12, 2025 · 5 min read
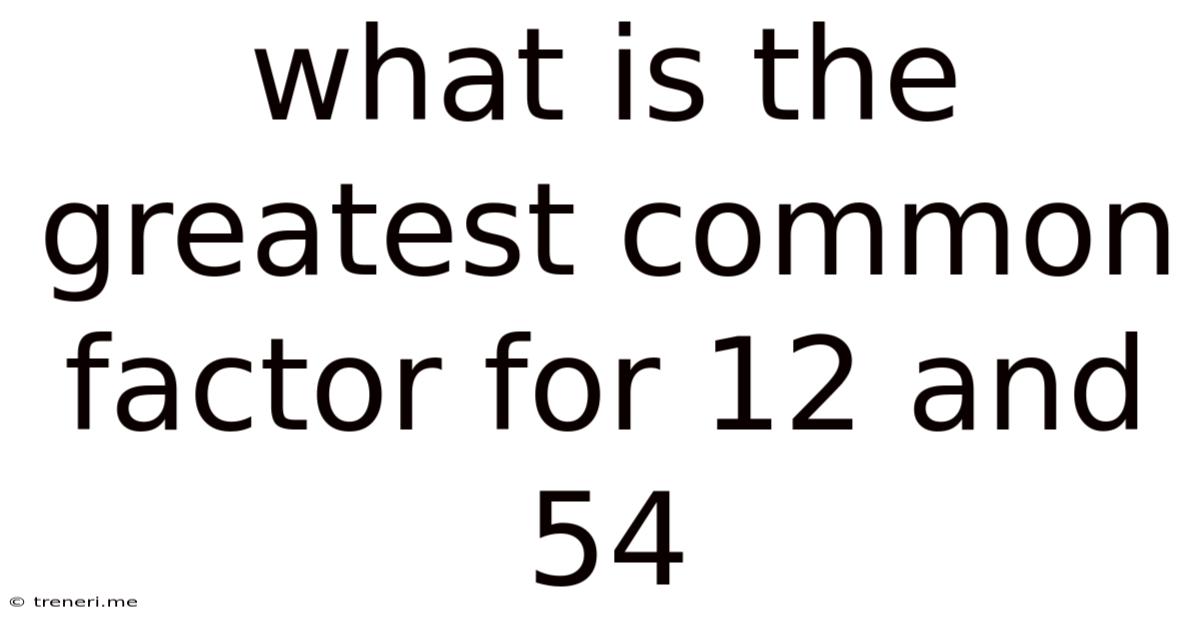
Table of Contents
What is the Greatest Common Factor for 12 and 54? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can significantly enhance your mathematical skills and problem-solving abilities. This comprehensive guide will delve into determining the GCF for 12 and 54, explaining multiple approaches, and demonstrating their practical applications beyond basic arithmetic. We'll also explore the broader concept of GCF and its significance in various mathematical contexts.
Understanding the Greatest Common Factor (GCF)
Before we tackle the specific problem of finding the GCF of 12 and 54, let's establish a firm understanding of what the GCF actually represents. The greatest common factor, also known as greatestcommon divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. This concept is fundamental in simplifying fractions, solving algebraic equations, and even in more advanced areas of mathematics like abstract algebra.
Method 1: Prime Factorization
This method is considered a cornerstone in determining the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to 12 and 54:
Prime Factorization of 12:
12 can be factored as follows:
- 12 = 2 x 6
- 12 = 2 x 2 x 3
- 12 = 2² x 3
Therefore, the prime factorization of 12 is 2² x 3.
Prime Factorization of 54:
Now let's break down 54:
- 54 = 2 x 27
- 54 = 2 x 3 x 9
- 54 = 2 x 3 x 3 x 3
- 54 = 2 x 3³
The prime factorization of 54 is 2 x 3³.
Finding the GCF using Prime Factorization:
Once we have the prime factorizations, finding the GCF becomes straightforward. We identify the common prime factors and multiply them together, using the lowest power of each common factor.
Both 12 and 54 share a common factor of 2 and 3. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹.
Therefore, the GCF of 12 and 54 is 2 x 3 = 6.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor. While effective for smaller numbers, it can become cumbersome for larger ones.
Factors of 12:
1, 2, 3, 4, 6, 12
Factors of 54:
1, 2, 3, 6, 9, 18, 27, 54
Identifying the GCF:
By comparing the lists, we can see that the common factors of 12 and 54 are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 54 is 6.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the GCF, especially when dealing with larger numbers. It relies on repeated application of the division algorithm.
The algorithm works as follows:
- Divide the larger number by the smaller number and find the remainder.
- Replace the larger number with the smaller number and the smaller number with the remainder.
- Repeat steps 1 and 2 until the remainder is 0.
- The last non-zero remainder is the GCF.
Let's apply this to 12 and 54:
- 54 ÷ 12 = 4 with a remainder of 6.
- Now we consider 12 and 6.
- 12 ÷ 6 = 2 with a remainder of 0.
Since the remainder is 0, the last non-zero remainder (6) is the GCF. Therefore, the GCF of 12 and 54 is 6.
Applications of the Greatest Common Factor
The GCF finds applications in various mathematical contexts, extending far beyond simple arithmetic exercises. Here are some key applications:
-
Simplifying Fractions: The GCF is crucial for reducing fractions to their simplest form. For example, the fraction 12/54 can be simplified by dividing both the numerator and denominator by their GCF, which is 6. This simplifies the fraction to 2/9.
-
Solving Algebraic Equations: The GCF plays a role in factoring algebraic expressions. Finding the GCF of the terms in an expression allows you to factor it and simplify equations.
-
Geometry and Measurement: The GCF is often used in geometry problems involving finding the greatest possible side length of identical squares that can be used to tile a rectangle.
-
Number Theory: The GCF is a fundamental concept in number theory, a branch of mathematics dealing with the properties of integers.
-
Computer Science: Algorithms for finding the GCF are used in various computer science applications, including cryptography and data compression.
Beyond the Basics: Extending GCF Concepts
The concept of the GCF can be extended to more than two numbers. To find the GCF of multiple numbers, you can use any of the methods described above, but you'll need to apply them iteratively. For example, to find the GCF of 12, 54, and 18, you would first find the GCF of 12 and 54 (which is 6), and then find the GCF of 6 and 18 (which is 6).
Another important concept related to the GCF is the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of all the integers in a set. The GCF and LCM are related through the following formula:
LCM(a, b) x GCF(a, b) = a x b
Understanding this relationship allows you to easily calculate the LCM if you already know the GCF (or vice-versa).
Conclusion: Mastering GCF for Enhanced Mathematical Skills
Finding the greatest common factor is a fundamental skill in mathematics. This guide has explored multiple methods for determining the GCF, including prime factorization, listing factors, and the Euclidean algorithm, each offering its own advantages depending on the complexity of the numbers involved. Understanding the different methods not only helps you solve specific problems but also deepens your overall mathematical comprehension. The ability to find the GCF is not just a theoretical concept; it has practical applications across numerous fields, highlighting its significance in both academic and real-world scenarios. By mastering these techniques, you'll build a solid foundation for tackling more advanced mathematical challenges. The seemingly simple task of finding the GCF opens doors to a wider understanding of numbers and their relationships, empowering you with valuable problem-solving skills applicable well beyond the realm of arithmetic.
Latest Posts
Latest Posts
-
How Much Is 1000ml In Oz
May 12, 2025
-
What Is The Greatest Common Factor Of 3 And 15
May 12, 2025
-
1 2 Yard To Cubic Feet
May 12, 2025
-
How Many Calories Does A Steam Room Burn
May 12, 2025
-
Cuanto Es Grados Centigrados En Fahrenheit
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor For 12 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.