What Is The Greatest Common Factor Of 12 And 54
Treneri
May 14, 2025 · 5 min read
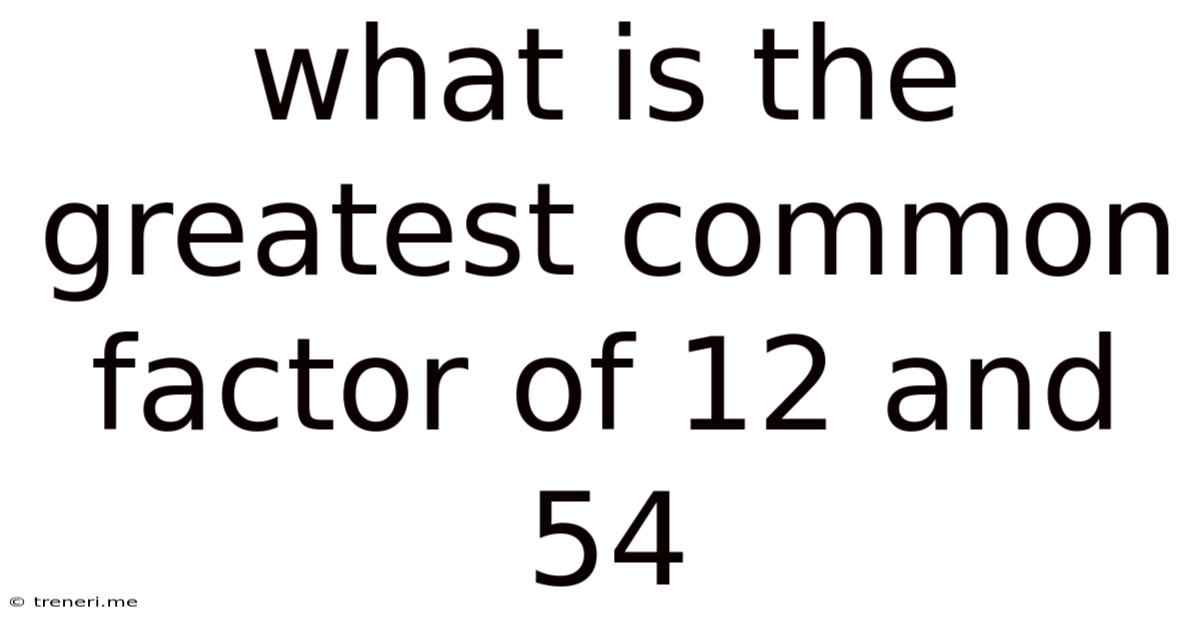
Table of Contents
What is the Greatest Common Factor of 12 and 54? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and different methods for solving it opens up a world of mathematical understanding. This article delves deep into finding the GCF of 12 and 54, exploring multiple approaches and highlighting their practical applications in various mathematical contexts. We'll also examine the significance of GCF in simplifying fractions, factoring polynomials, and solving more complex mathematical problems.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the highest common factor (HCF) or greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. In simpler terms, it's the biggest number that is a factor of both numbers.
For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54. The common factors of 12 and 54 are 1, 2, 3, and 6. The greatest among these is 6. Therefore, the GCF of 12 and 54 is 6.
Methods for Finding the GCF
Several methods can efficiently determine the GCF of two numbers. Let's explore the most common ones:
1. Listing Factors Method
This is the most straightforward method, especially for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
- Common Factors: 1, 2, 3, 6
- Greatest Common Factor: 6
This method is effective for smaller numbers but becomes cumbersome with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime Factorization of 12: 2² × 3
- Prime Factorization of 54: 2 × 3³
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹. Multiplying these together gives 2 × 3 = 6. Therefore, the GCF of 12 and 54 is 6.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 12 and 54:
- 54 = 12 × 4 + 6 (Divide 54 by 12; the remainder is 6)
- 12 = 6 × 2 + 0 (Divide 12 by 6; the remainder is 0)
The last non-zero remainder is 6, which is the GCF of 12 and 54.
This method is highly efficient, even for very large numbers, as it avoids the need to find all factors.
Applications of GCF
Understanding and calculating the GCF has numerous applications in various areas of mathematics and beyond:
1. Simplifying Fractions
The GCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF.
For example, consider the fraction 12/54. The GCF of 12 and 54 is 6. Dividing both the numerator and denominator by 6 gives us 2/9, the simplified form of the fraction.
2. Factoring Polynomials
GCF is essential in factoring polynomials. When factoring a polynomial, we look for the greatest common factor among all the terms. We then factor out the GCF, leaving the remaining terms in parentheses.
For example, consider the polynomial 12x² + 54x. The GCF of 12x² and 54x is 6x. Factoring out 6x, we get 6x(2x + 9).
3. Solving Word Problems
Many word problems involve finding the GCF to solve them efficiently. For instance, problems related to dividing objects into equal groups or finding the largest possible size of square tiles to cover a rectangular area often require finding the GCF.
4. Number Theory
GCF is a fundamental concept in number theory, forming the basis for many advanced mathematical theorems and concepts. For example, it's used in modular arithmetic and in solving Diophantine equations.
5. Cryptography
Surprisingly, GCF finds its way into cryptography, particularly in RSA encryption. The security of the RSA algorithm relies heavily on the difficulty of finding the GCF of two very large numbers.
Beyond the Basics: Exploring Further Concepts Related to GCF
The concept of GCF extends beyond simply finding the greatest common factor of two numbers. Let's explore some related ideas:
-
Least Common Multiple (LCM): The least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. The GCF and LCM are related through the equation: GCF(a, b) × LCM(a, b) = a × b. This relationship is incredibly useful in solving various mathematical problems.
-
GCF of More Than Two Numbers: The concept of GCF can be easily extended to more than two numbers. We find the prime factorization of each number and then select the common prime factors raised to the lowest power.
-
GCF in Different Number Systems: The concept of GCF isn't limited to the decimal number system. We can find the GCF of numbers in other number systems, such as binary or hexadecimal systems.
Conclusion: The Practical Power of GCF
The greatest common factor, while seemingly a simple concept, is a fundamental building block in numerous mathematical areas. Understanding the different methods for finding the GCF, from listing factors to the efficient Euclidean algorithm, empowers us to solve a wide range of problems, from simplifying fractions to factoring polynomials and even contributing to the security of cryptographic systems. Mastering the concept of GCF enhances our mathematical abilities and provides a solid foundation for tackling more complex mathematical concepts in the future. This deep dive has highlighted the multifaceted nature of GCF and its pervasive role in the world of numbers. From the simple task of simplifying a fraction to the intricate workings of cryptography, the GCF remains a cornerstone of mathematical understanding.
Latest Posts
Latest Posts
-
How Much More Time Until 12 Pm
May 14, 2025
-
1984 A 2024 Cuantos Anos Son
May 14, 2025
-
How Many Hours Is In 17 Days
May 14, 2025
-
How To Find Speed With Acceleration And Time
May 14, 2025
-
33 Km To Miles Per Hour
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 12 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.