What Is The Greatest Common Factor Of 15 And 3
Treneri
May 10, 2025 · 6 min read
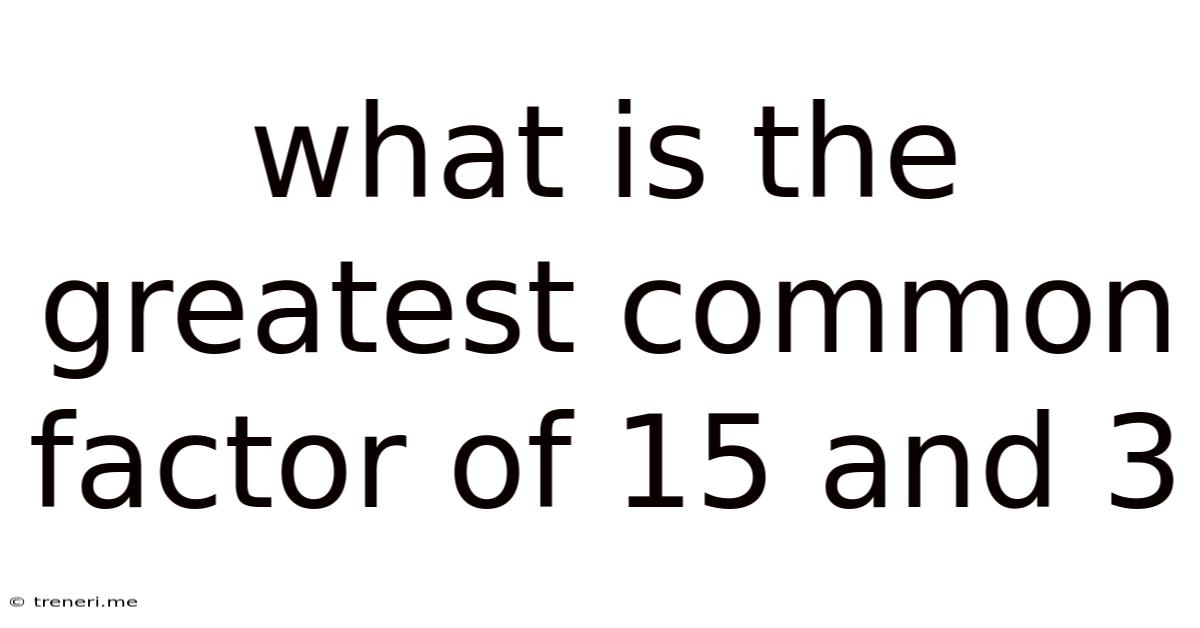
Table of Contents
What is the Greatest Common Factor of 15 and 3? A Deep Dive into Finding GCFs
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles and various methods for calculating it offers valuable insights into number theory and its applications. This article delves deep into the concept of GCF, specifically focusing on finding the greatest common factor of 15 and 3, while also exploring broader techniques applicable to any pair of numbers. We’ll explore different methods, discuss their advantages and disadvantages, and even touch on the historical context and practical applications of GCFs.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving any remainder.
Key Concepts:
- Factors: Factors are numbers that divide another number evenly. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
- Common Factors: These are factors that are shared by two or more numbers. For example, the common factors of 12 and 18 are 1, 2, 3, and 6.
- Greatest Common Factor (GCF): The largest of the common factors.
Finding the GCF of 15 and 3: Methods and Approaches
Now, let's focus on finding the GCF of 15 and 3. This specific example allows us to illustrate several methods effectively, showcasing their simplicity and efficiency.
Method 1: Listing Factors
This is the most straightforward approach, especially for smaller numbers. We list all the factors of each number and then identify the largest common factor.
- Factors of 15: 1, 3, 5, 15
- Factors of 3: 1, 3
The common factors are 1 and 3. The greatest of these is 3. Therefore, the GCF of 15 and 3 is 3.
Method 2: Prime Factorization
This method is particularly useful for larger numbers. We find the prime factorization of each number (expressing them as a product of prime numbers) and then identify the common prime factors raised to the lowest power.
- Prime factorization of 15: 3 x 5
- Prime factorization of 3: 3
The only common prime factor is 3. Therefore, the GCF of 15 and 3 is 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, especially for larger numbers. It's based on repeated division with remainder. The algorithm proceeds as follows:
- Divide the larger number (15) by the smaller number (3).
- If the remainder is 0, the smaller number is the GCF.
- If the remainder is not 0, replace the larger number with the smaller number and the smaller number with the remainder. Repeat steps 1 and 2.
Let's apply it to 15 and 3:
- 15 ÷ 3 = 5 with a remainder of 0.
Since the remainder is 0, the GCF is the smaller number, which is 3.
Advantages and Disadvantages of Each Method
Let's compare the three methods:
| Method | Advantages | Disadvantages | Best Suited For |
|---|---|---|---|
| Listing Factors | Simple, easy to understand for small numbers | Inefficient for large numbers | Small numbers |
| Prime Factorization | Efficient for larger numbers, reveals prime structure | Requires knowledge of prime factorization | Larger numbers, understanding prime numbers |
| Euclidean Algorithm | Very efficient for large numbers, systematic approach | Can be slightly more complex to grasp initially | Large numbers, computational efficiency needed |
Why Understanding GCF is Important
The GCF has numerous applications in various fields:
-
Simplifying Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For example, the fraction 15/3 can be simplified to 5/1 (or simply 5) by dividing both the numerator and denominator by their GCF, which is 3.
-
Solving Algebraic Equations: GCF plays a crucial role in factoring algebraic expressions, which is essential for solving many types of equations.
-
Geometry and Measurement: GCF is used in geometry problems involving area and perimeter calculations, and in scenarios where we need to find the largest common divisor for measurements. For example, finding the largest square tile that can perfectly cover a rectangular floor with dimensions 15 feet by 3 feet. The answer is a square tile of 3 feet by 3 feet.
-
Computer Science: The GCF is used in various algorithms and computations, especially in cryptography and number theory-based applications.
GCF in Everyday Life: Real-World Applications
While it might not be immediately obvious, the concept of GCF subtly appears in everyday life:
-
Sharing Equally: Imagine you have 15 apples and you want to distribute them equally among 3 friends. The GCF (3) tells you that each friend will receive 5 apples.
-
Dividing Resources: If you have 15 meters of fabric and you want to cut it into pieces of 3 meters each, the GCF helps you determine the number of pieces you can make (5 pieces).
Historical Context: A Glimpse into the Past
The concept of GCF has a rich history, tracing back to ancient civilizations. The Euclidean algorithm, a powerful method for calculating the GCF, is named after the ancient Greek mathematician Euclid, who described it in his seminal work Elements around 300 BC. This algorithm remains remarkably efficient even today, demonstrating the enduring power of mathematical principles. Ancient Babylonian and Egyptian mathematicians also possessed methods for finding GCFs, highlighting the fundamental nature of this concept throughout history.
Expanding the Concept: GCFs of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 15, 3, and 9:
- Listing Factors: List the factors of each number and find the largest common factor.
- Prime Factorization: Find the prime factorization of each number and identify the common prime factors raised to the lowest power.
- Euclidean Algorithm (extended): Repeatedly apply the Euclidean algorithm to pairs of numbers until you find the GCF of all numbers. In this case, we can find the GCF of 15 and 3 (which is 3), and then find the GCF of 3 and 9 (which is 3). Therefore, the GCF of 15, 3, and 9 is 3.
Conclusion: The Enduring Relevance of the GCF
The greatest common factor, while seemingly a simple concept, possesses a depth and versatility that extends far beyond basic arithmetic. From simplifying fractions to solving complex equations, its applications are widespread and impactful. Understanding the different methods for calculating the GCF, their advantages, and their historical significance provides a richer appreciation for this fundamental concept in number theory and its relevance to various fields. The GCF is not just a mathematical tool; it's a cornerstone of mathematical reasoning and problem-solving. The simple example of finding the GCF of 15 and 3 serves as a powerful entry point into this fascinating realm of mathematics, revealing its beauty and practical value.
Latest Posts
Latest Posts
-
7 15 Divided By 3 10 As A Fraction
May 10, 2025
-
Gcf Of 75 8 And 21
May 10, 2025
-
How Much Is 160ml In Cups
May 10, 2025
-
Cuanto Es 10 Yardas En Pies
May 10, 2025
-
What Is A Good Keystroke Per Hour
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 15 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.