What Is The Greatest Common Factor Of 15 And 6
Treneri
May 12, 2025 · 5 min read
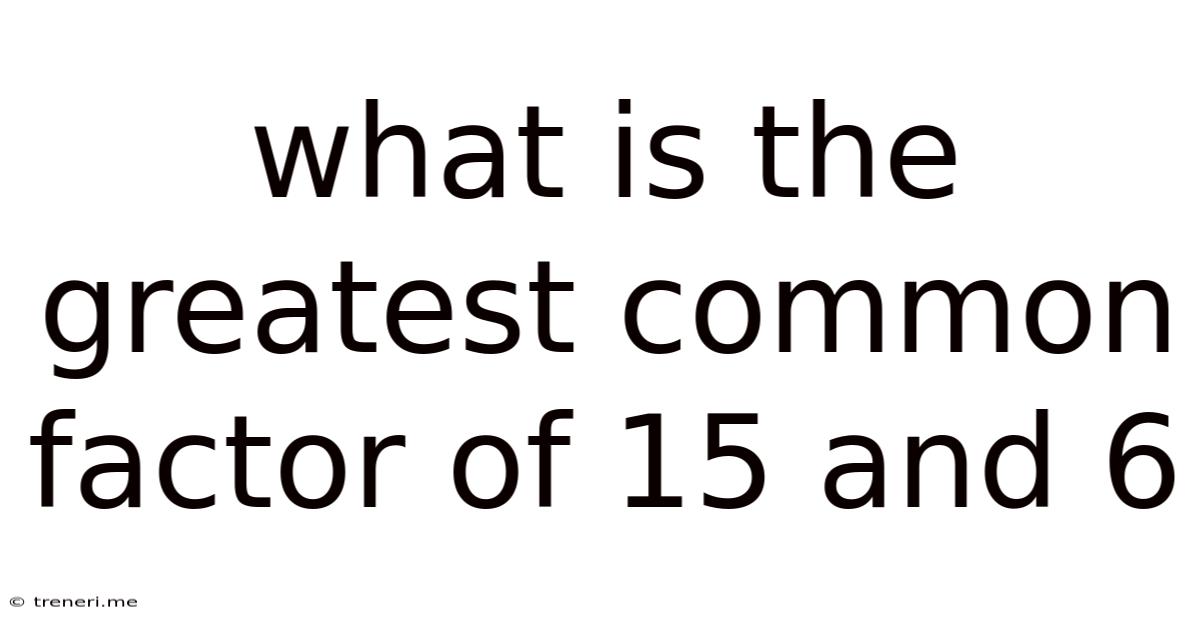
Table of Contents
What is the Greatest Common Factor of 15 and 6? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods opens up a world of mathematical understanding with applications far beyond basic number theory. This comprehensive guide will delve into the process of finding the GCF of 15 and 6, explaining multiple approaches and showcasing the broader significance of this concept in mathematics.
Understanding the Greatest Common Factor (GCF)
The greatest common factor, also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. In simpler terms, it's the biggest number that is a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
This concept is crucial in various mathematical fields, including:
- Simplifying fractions: Finding the GCF helps reduce fractions to their simplest form.
- Algebraic expressions: GCF is essential for factoring algebraic expressions, simplifying equations, and solving problems.
- Geometry: Determining the dimensions of shapes often involves finding the GCF.
- Number theory: GCF forms the basis of numerous theorems and algorithms in number theory.
Methods for Finding the GCF of 15 and 6
Let's explore several ways to determine the GCF of 15 and 6:
1. Listing Factors
This is a straightforward method, especially for smaller numbers:
- Factors of 15: 1, 3, 5, 15
- Factors of 6: 1, 2, 3, 6
The common factors are 1 and 3. The greatest of these is 3. Therefore, the GCF of 15 and 6 is 3.
2. Prime Factorization
Prime factorization involves expressing each number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 15: 3 x 5
- Prime factorization of 6: 2 x 3
The common prime factor is 3. Therefore, the GCF of 15 and 6 is 3. This method becomes more efficient when dealing with larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors becomes cumbersome. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply it to 15 and 6:
- 15 ÷ 6 = 2 with a remainder of 3
- 6 ÷ 3 = 2 with a remainder of 0
Since the remainder is 0, the GCF is the last non-zero remainder, which is 3.
4. Venn Diagrams
Venn diagrams provide a visual representation of the factors and help identify the common factors. Draw two overlapping circles, one for the factors of 15 and one for the factors of 6. The overlapping section represents the common factors.
- Circle 1 (15): 1, 3, 5, 15
- Circle 2 (6): 1, 2, 3, 6
- Overlapping section: 1, 3
The largest number in the overlapping section is 3, confirming that the GCF of 15 and 6 is 3.
Applications of GCF in Real-World Scenarios
The seemingly simple concept of GCF has far-reaching applications in various practical scenarios:
-
Baking: Imagine you're baking cookies and have 15 chocolate chips and 6 raisins. To distribute them evenly across several cookies, you need to find the GCF (which is 3). You can make 3 cookies, each with 5 chocolate chips and 2 raisins.
-
Gardening: You have 15 red flowers and 6 yellow flowers, and you want to plant them in rows with an equal number of each color flower in each row. The GCF (3) tells you that you can make 3 rows, each with 5 red flowers and 2 yellow flowers.
-
Construction: You're building a patio using tiles that are 15 cm and 6 cm wide. To maintain a uniform pattern, you'd use tiles with a width equal to their GCF (3 cm).
-
Resource Allocation: Distributing resources fairly among groups often involves finding the GCF to ensure equitable distribution.
Expanding on the Concept: GCF of More Than Two Numbers
The principles of finding the GCF can be extended to more than two numbers. You can use any of the methods mentioned above, but prime factorization often becomes the most efficient approach for larger sets of numbers. For instance, to find the GCF of 15, 6, and 30:
-
Prime factorization:
- 15 = 3 x 5
- 6 = 2 x 3
- 30 = 2 x 3 x 5
-
Identify common prime factors: The common prime factor is 3.
-
GCF: The GCF of 15, 6, and 30 is 3.
Beyond the Basics: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). While the GCF is the largest number that divides both numbers, the LCM is the smallest number that is a multiple of both numbers. Finding the LCM is crucial in operations involving fractions, particularly when adding or subtracting fractions with different denominators.
The relationship between GCF and LCM is expressed by the following formula:
LCM(a, b) x GCF(a, b) = a x b
For 15 and 6:
- GCF(15, 6) = 3
- LCM(15, 6) = (15 x 6) / 3 = 30
This formula highlights the interconnectedness of these two important concepts in number theory.
Conclusion: The Significance of GCF
The greatest common factor is a fundamental concept in mathematics with applications spanning various fields. Understanding the different methods for finding the GCF, from simple listing of factors to the efficient Euclidean algorithm, provides a solid foundation for tackling more complex mathematical problems. Its practical applications in everyday life demonstrate the relevance of seemingly abstract mathematical concepts. The relationship between GCF and LCM further enriches the understanding of number theory and its essential role in solving various mathematical challenges. Mastering the GCF concept opens doors to a deeper appreciation of mathematical principles and their significant role in our world.
Latest Posts
Latest Posts
-
How Many Months Is 42 Years
May 13, 2025
-
How Do You Find The Height Of A Square
May 13, 2025
-
How Many Cups Is A 1 2 Gallon
May 13, 2025
-
Born In June 1982 How Old Am I
May 13, 2025
-
How Many Degrees Is A 6 12 Pitch
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 15 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.