What Is The Greatest Common Factor Of 15 And 9
Treneri
May 13, 2025 · 5 min read
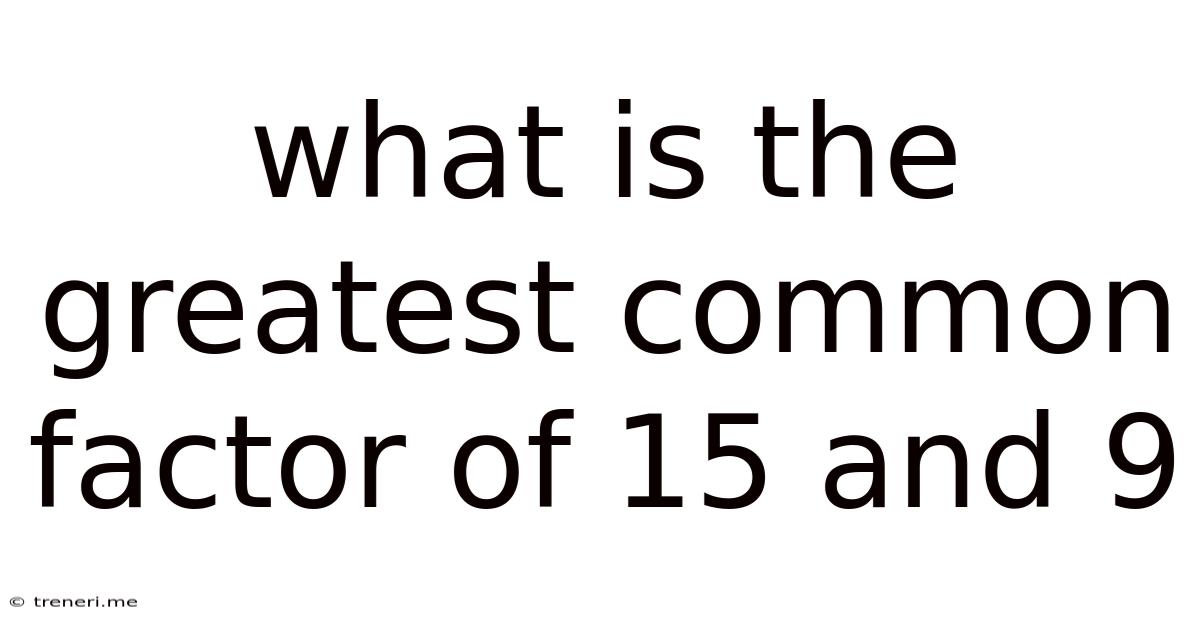
Table of Contents
What is the Greatest Common Factor of 15 and 9? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with applications far beyond basic math. This in-depth exploration delves into the GCF of 15 and 9, explaining multiple methods for calculating it and showcasing its relevance in various mathematical contexts.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific case of 15 and 9, let's solidify our understanding of GCFs. The greatest common factor, also known as the greatest common divisor (GCD), is the largest positive integer that divides both of the given integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
Key Characteristics of GCF:
- Divisibility: The GCF must be a divisor of both numbers.
- Greatest: It's the largest such divisor.
- Uniqueness: For any two positive integers, there's only one GCF.
Method 1: Listing Factors
The most straightforward method, particularly for smaller numbers like 15 and 9, is to list all the factors of each number and identify the largest one they share.
Factors of 15: 1, 3, 5, 15 Factors of 9: 1, 3, 9
Comparing the two lists, we see that the common factors are 1 and 3. The largest of these is 3.
Therefore, the greatest common factor of 15 and 9 is 3.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves breaking down each number into its prime factors – prime numbers that multiply together to give the original number.
Prime Factorization of 15: 3 x 5 Prime Factorization of 9: 3 x 3
To find the GCF, we identify the common prime factors and multiply them together. Both 15 and 9 share one factor of 3. Therefore, the GCF is 3.
This method becomes particularly useful when dealing with larger numbers where listing all factors would be tedious. For instance, finding the GCF of 105 and 165:
Prime Factorization of 105: 3 x 5 x 7 Prime Factorization of 165: 3 x 5 x 11
The common prime factors are 3 and 5. Multiplying these gives us 15, so the GCF of 105 and 165 is 15.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, especially for larger numbers, to find the GCF. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply this to 15 and 9:
- Start with the larger number (15) and the smaller number (9).
- Subtract the smaller number from the larger number: 15 - 9 = 6.
- Replace the larger number with the result (6), and keep the smaller number (9). Now we have 9 and 6.
- Repeat: 9 - 6 = 3.
- Repeat: 6 - 3 = 3.
- The process stops when both numbers are equal, which is 3.
Therefore, the GCF of 15 and 9 is 3.
The Euclidean algorithm is particularly efficient because it avoids the need for complete prime factorization, making it significantly faster for large numbers.
Applications of GCF
The concept of the greatest common factor extends far beyond basic arithmetic. Here are some key applications:
1. Simplifying Fractions
GCFs are crucial for simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and the denominator by their GCF. For example:
15/9 = (15 ÷ 3) / (9 ÷ 3) = 5/3
2. Solving Word Problems
Many word problems involving quantities that need to be divided equally require finding the GCF. For instance, if you have 15 apples and 9 oranges and you want to make bags with the same number of apples and oranges in each bag, finding the GCF (3) will tell you that you can make 3 bags.
3. Geometry
GCFs are used in geometry problems dealing with finding the largest square tile that can be used to completely cover a rectangular area. For example, if you have a rectangle of dimensions 15cm by 9cm, the largest square tile you can use has a side length of 3cm (the GCF of 15 and 9).
4. Music Theory
In music, GCFs help determine the greatest common divisor of note durations, assisting in the simplification of rhythmic notation.
5. Cryptography
Concepts related to GCFs, such as the Euclidean algorithm, are fundamental in modern cryptography, particularly in public-key cryptography. These algorithms are the backbone of secure online transactions and communication.
Beyond the Basics: Extending the Concept
The GCF concept extends to more than two numbers. We can find the GCF of multiple integers by repeatedly applying the methods discussed above. For instance, to find the GCF of 15, 9, and 6:
- Find the GCF of 15 and 9 (which is 3).
- Find the GCF of 3 and 6 (which is 3).
Therefore, the GCF of 15, 9, and 6 is 3.
Furthermore, the concept of GCF lays the foundation for understanding other important concepts in number theory such as the least common multiple (LCM), which is the smallest number that is a multiple of both given numbers. The relationship between GCF and LCM is expressed as: GCF(a, b) * LCM(a, b) = a * b
Conclusion: The Importance of GCF
The seemingly simple calculation of the greatest common factor is a cornerstone of number theory with significant applications in various fields. Mastering different methods for finding the GCF, such as listing factors, prime factorization, and the Euclidean algorithm, provides a strong foundation for tackling more complex mathematical problems and understanding the underlying structure of numbers. The GCF’s practical applications range from simplifying fractions to its crucial role in modern cryptography, highlighting its enduring importance in mathematics and beyond. Understanding the GCF is not merely about finding a single answer; it's about grasping a fundamental concept that unlocks a deeper understanding of the world of numbers.
Latest Posts
Latest Posts
-
How To Calculate The Flow Rate Of Water
May 13, 2025
-
How Many Tablespoons Is 3 Cloves Of Garlic Minced
May 13, 2025
-
Round 475 To The Nearest Ten
May 13, 2025
-
1 Pint Heavy Cream To Cups
May 13, 2025
-
How Old Am I If I Was Born In 62
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 15 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.