What Is The Greatest Common Factor Of 18 And 60
Treneri
May 14, 2025 · 5 min read
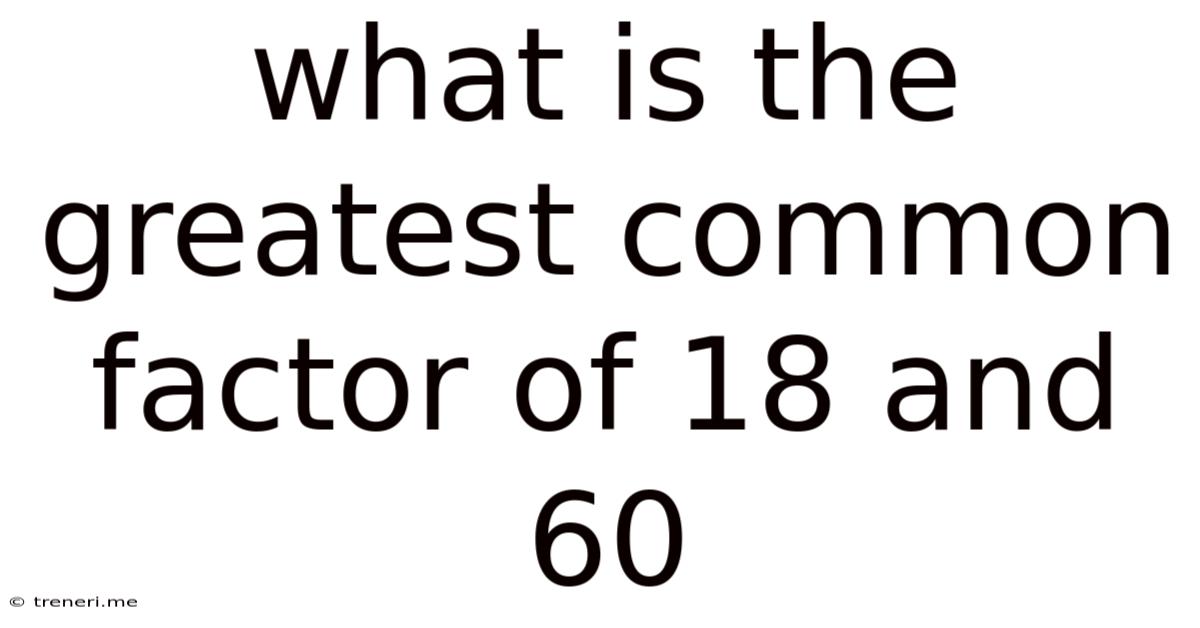
Table of Contents
What is the Greatest Common Factor of 18 and 60? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical possibilities. This article delves into the various methods of determining the GCF of 18 and 60, exploring the theoretical underpinnings and practical applications along the way. We'll move beyond simply stating the answer and illuminate the rich mathematical landscape surrounding this seemingly basic concept.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding the GCF is crucial in various mathematical fields, including simplification of fractions, solving equations, and even in more advanced areas like abstract algebra.
Why is finding the GCF important?
Finding the GCF offers several practical applications:
-
Simplifying Fractions: Reducing fractions to their simplest form relies heavily on finding the GCF of the numerator and denominator. For example, simplifying 18/60 requires finding the GCF, which allows us to express the fraction in its most concise form.
-
Solving Equations: In certain algebraic equations, determining the GCF helps in factoring expressions, simplifying solutions, and making the equation easier to manipulate.
-
Problem Solving: Many real-world problems, from dividing resources equally to arranging objects in patterns, involve finding the GCF.
-
Number Theory: The GCF is a fundamental concept in number theory, laying the groundwork for understanding more complex number relationships and properties.
Methods for Finding the GCF of 18 and 60
Several methods exist for determining the GCF of two numbers. Let's explore the most common techniques, applying them to find the GCF of 18 and 60.
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 18: 1, 2, 3, 6, 9, 18 Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
By comparing the lists, we can see that the common factors are 1, 2, 3, and 6. The greatest common factor is therefore 6.
This method is straightforward for smaller numbers, but it becomes less efficient as the numbers increase in size.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The prime factorization of a number is its expression as a product of prime numbers (numbers divisible only by 1 and themselves).
Prime Factorization of 18: 2 x 3 x 3 = 2 x 3² Prime Factorization of 60: 2 x 2 x 3 x 5 = 2² x 3 x 5
To find the GCF using prime factorization, we identify the common prime factors and their lowest powers. Both 18 and 60 share a '2' and a '3'. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹. Therefore, the GCF is 2 x 3 = 6.
This method is more efficient for larger numbers than listing factors, especially when dealing with numbers that have many factors.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 18 and 60:
- 60 - 18 = 42 (Now we find the GCF of 18 and 42)
- 42 - 18 = 24 (Now we find the GCF of 18 and 24)
- 24 - 18 = 6 (Now we find the GCF of 18 and 6)
- 18 - 6 = 12 (Now we find the GCF of 6 and 12)
- 12 - 6 = 6 (Now we find the GCF of 6 and 6)
Since both numbers are now equal to 6, the GCF of 18 and 60 is 6.
The Euclidean algorithm is particularly useful for larger numbers because it significantly reduces the number of steps compared to other methods.
Applications of the GCF of 18 and 60
Now that we've established that the GCF of 18 and 60 is 6, let's explore some practical applications:
Simplifying Fractions
Consider the fraction 18/60. By dividing both the numerator and the denominator by their GCF (6), we simplify the fraction:
18 ÷ 6 = 3 60 ÷ 6 = 10
Therefore, 18/60 simplifies to 3/10.
Dividing Objects Equally
Imagine you have 18 apples and 60 oranges. You want to divide them into identical bags, with the same number of apples and oranges in each bag. The GCF (6) tells you that you can create 6 identical bags, each containing 3 apples and 10 oranges.
Extending the Concept: Beyond Two Numbers
The concept of the GCF extends beyond two numbers. We can find the GCF of multiple numbers by applying the same principles. For instance, to find the GCF of 18, 60, and 90, we can use prime factorization or the Euclidean algorithm repeatedly.
Conclusion: The Power of the GCF
Determining the greatest common factor of 18 and 60, as we've seen, is more than just a simple arithmetic exercise. It showcases fundamental concepts in number theory and provides a foundation for more complex mathematical operations. Understanding the various methods for finding the GCF – listing factors, prime factorization, and the Euclidean algorithm – equips us to solve problems efficiently, regardless of the size of the numbers involved. From simplifying fractions to dividing resources equally, the GCF plays a significant, often unnoticed, role in our daily mathematical encounters. Its importance extends far beyond elementary arithmetic, illustrating the interconnectedness and power of fundamental mathematical principles.
Latest Posts
Latest Posts
-
How Long Would It Take To Travel 7 Trillion Miles
May 15, 2025
-
What Is The Reciprocal Of 5 7
May 15, 2025
-
56 6 Liters Of Mulch To Pounds
May 15, 2025
-
54 Out Of 80 As A Percentage
May 15, 2025
-
How Many More Hours Until 5 Am
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 18 And 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.