What Is The Greatest Common Factor Of 19 And 38
Treneri
May 12, 2025 · 5 min read
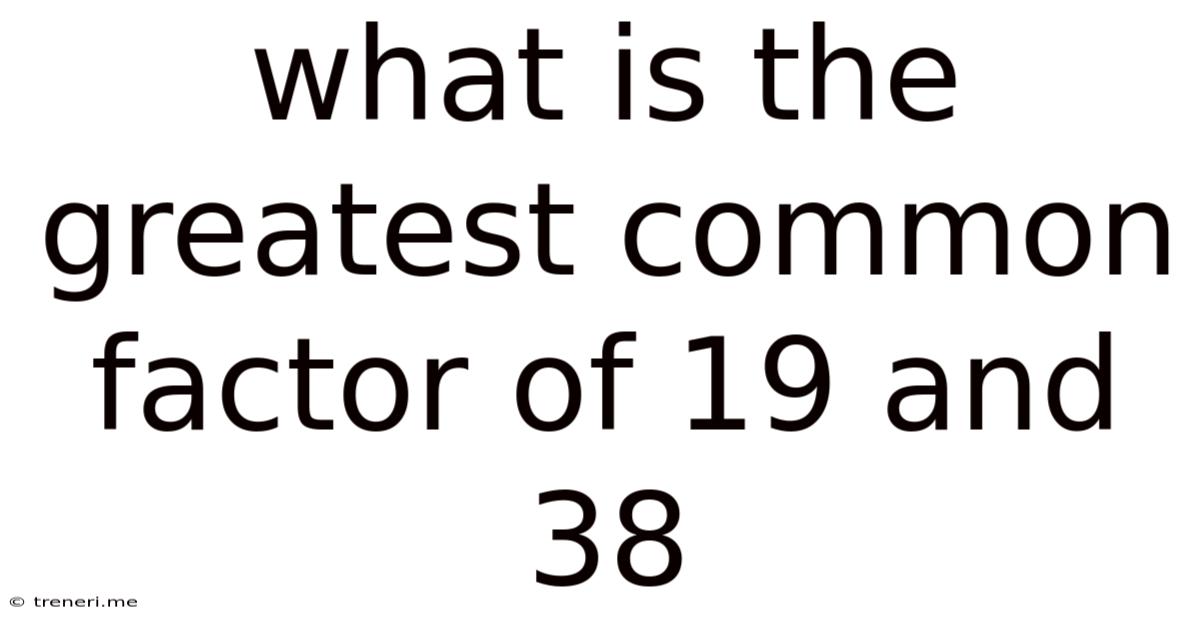
Table of Contents
What is the Greatest Common Factor of 19 and 38? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a concept that underpins much of number theory and has practical applications in various fields. This article delves deep into determining the GCF of 19 and 38, explaining the process, exploring different methods, and expanding on the broader significance of GCFs in mathematics.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can be divided evenly into both numbers. This concept is fundamental to simplifying fractions, solving algebraic equations, and understanding relationships between numbers.
Methods for Finding the GCF
Several methods exist for finding the GCF, each with its own advantages and disadvantages. Let's explore some of the most common techniques:
1. Listing Factors Method
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 19: 1, 19 Factors of 38: 1, 2, 19, 38
The common factors are 1 and 19. Therefore, the GCF of 19 and 38 is 19.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors – prime numbers that multiply together to give the original number. The GCF is then found by multiplying the common prime factors raised to the lowest power.
Prime Factorization of 19: 19 (19 is a prime number) Prime Factorization of 38: 2 x 19
The only common prime factor is 19. Therefore, the GCF of 19 and 38 is 19.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 19 and 38:
- 38 = 19 x 2 + 0
Since the remainder is 0, the GCF is the smaller number, which is 19.
Why is the GCF Important?
The GCF has numerous applications across various mathematical and practical contexts:
1. Simplifying Fractions
The GCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, if we had the fraction 38/19, we would divide both by their GCF (19), resulting in the simplified fraction 2/1, or simply 2.
2. Solving Algebraic Equations
GCFs are often used in factoring algebraic expressions, which is essential for solving many algebraic equations. By factoring out the GCF, we can simplify equations and make them easier to solve.
3. Number Theory and Cryptography
The concept of GCF is fundamental in number theory, forming the basis for many advanced theorems and algorithms. It also plays a significant role in cryptography, where the security of certain encryption methods relies on the difficulty of finding the GCF of very large numbers.
4. Real-World Applications
GCFs have practical applications in various fields, including:
- Geometry: Finding the dimensions of the largest square tile that can perfectly cover a rectangular floor.
- Measurement: Converting units of measurement – finding the largest common unit to simplify conversions.
- Scheduling: Determining the optimal time intervals for recurring events (e.g., finding the time when two machines will complete their cycles simultaneously).
Exploring the Relationship Between 19 and 38
The fact that the GCF of 19 and 38 is 19 highlights a specific mathematical relationship: 38 is a multiple of 19 (38 = 19 x 2). This means 19 is a divisor of 38, and consequently, the largest common divisor. This relationship is characteristic of any pair of numbers where one is a multiple of the other. In such cases, the smaller number will always be the GCF.
Expanding on Prime Numbers and Factorization
The prime factorization method emphasizes the importance of prime numbers in number theory. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Prime numbers are the building blocks of all other integers, as every composite number (a number that is not prime) can be uniquely expressed as a product of prime numbers (Fundamental Theorem of Arithmetic). Understanding prime factorization is crucial for many number theory problems, including finding GCFs and least common multiples (LCMs).
The Least Common Multiple (LCM) and its Relationship to GCF
While this article focuses on the GCF, it's important to briefly mention the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are related by the following equation:
LCM(a, b) x GCF(a, b) = a x b
In the case of 19 and 38:
GCF(19, 38) = 19 LCM(19, 38) = 38
Therefore, 19 x 38 = 722, and 19 x 38 = 722, confirming the relationship.
Conclusion: The Significance of a Simple Calculation
Determining the greatest common factor of 19 and 38, while seemingly a simple arithmetic exercise, offers a window into the fascinating world of number theory. The various methods for calculating the GCF, along with its broad applications in mathematics and beyond, demonstrate the fundamental importance of this concept in understanding numerical relationships and solving a variety of problems. From simplifying fractions to contributing to the security of cryptographic systems, the GCF plays a significant and often underestimated role in our mathematical landscape. Understanding this seemingly simple concept unlocks a deeper appreciation of the intricate connections within the realm of numbers.
Latest Posts
Latest Posts
-
Cuanto Son 32 Oz En Litros
May 14, 2025
-
60 Days After July 19 2024
May 14, 2025
-
Cuantas Onzas Tiene 3 Litros De Agua
May 14, 2025
-
What Time Will My Movie End Calculator Free
May 14, 2025
-
How Many Tables For 40 Guests
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 19 And 38 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.