What Is The Greatest Common Factor Of 21 And 40
Treneri
May 10, 2025 · 5 min read
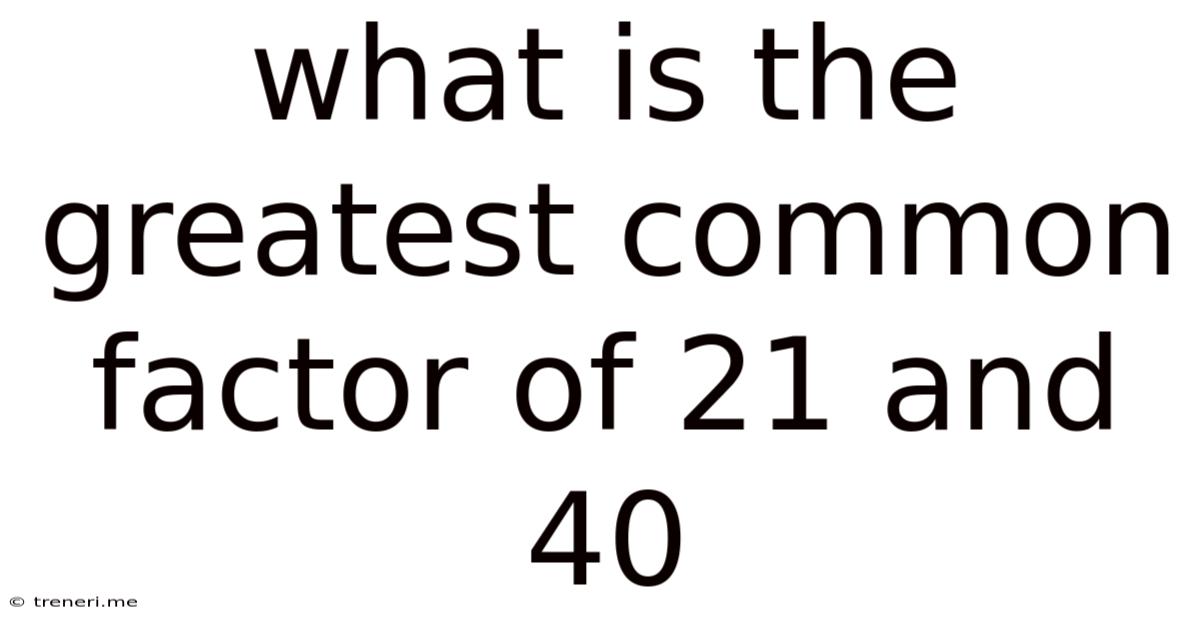
Table of Contents
What is the Greatest Common Factor of 21 and 40? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it underpins many important concepts in mathematics and computer science. This article will delve into the process of finding the GCF of 21 and 40, exploring different methods and highlighting the underlying principles of number theory. We'll also look at the practical applications of GCFs and related concepts.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. Therefore, the greatest common factor of 12 and 18 is 6.
Finding the GCF of 21 and 40: Method 1 - Listing Factors
The simplest method to find the GCF is by listing all the factors of each number and identifying the largest common one.
Factors of 21: 1, 3, 7, 21 Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Comparing the lists, we see that the only common factor of 21 and 40 is 1.
Therefore, the greatest common factor of 21 and 40 is 1.
Finding the GCF of 21 and 40: Method 2 - Prime Factorization
Prime factorization is a more powerful and efficient method, especially when dealing with larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Prime factorization of 21: 3 x 7 Prime factorization of 40: 2 x 2 x 2 x 5 = 2³ x 5
Notice that there are no common prime factors between 21 and 40. This confirms that their greatest common factor is 1. Numbers that share only 1 as their GCF are called relatively prime or coprime.
Finding the GCF of 21 and 40: Method 3 - Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 21 and 40:
- 40 = 1 x 21 + 19 (We subtract 21 from 40 once, leaving a remainder of 19)
- 21 = 1 x 19 + 2 (We subtract 19 from 21 once, leaving a remainder of 2)
- 19 = 9 x 2 + 1 (We subtract 2 from 19 nine times, leaving a remainder of 1)
- 2 = 2 x 1 + 0 (We subtract 1 from 2 twice, leaving a remainder of 0)
The last non-zero remainder is the GCF. In this case, the GCF of 21 and 40 is 1.
Applications of GCF
The concept of the greatest common factor has numerous applications across various fields:
1. Simplifying Fractions:
GCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, you divide both the numerator and the denominator by their GCF. For example, to simplify the fraction 12/18, we find the GCF of 12 and 18, which is 6. Dividing both the numerator and denominator by 6 gives us the simplified fraction 2/3.
2. Solving Word Problems:
Many word problems in mathematics involve finding the GCF. For example, consider a problem where you need to divide a certain number of items into groups of equal size, with no items left over. The GCF helps determine the largest possible group size.
3. Cryptography:
GCF and related concepts like the least common multiple (LCM) are fundamental in cryptography, which involves secure communication techniques. Algorithms for encryption and decryption rely on the properties of prime numbers and their relationships.
4. Computer Science:
GCF calculations are used in various computer science algorithms, such as those related to data structures and algorithm optimization.
Least Common Multiple (LCM) and its relationship with GCF
While we've focused on GCF, it's important to understand its relationship with the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is divisible by both numbers.
There's a simple relationship between GCF and LCM:
LCM(a, b) x GCF(a, b) = a x b
For 21 and 40:
- GCF(21, 40) = 1
- LCM(21, 40) = 840 (21 x 40 = 840; 840 / 1 = 840)
This formula is useful for calculating either the LCM or GCF if the other is known.
Beyond the Basics: Exploring Advanced Concepts
The concepts discussed above form the foundation for understanding more advanced topics in number theory:
- Modular Arithmetic: This involves working with remainders after division. GCF plays a significant role in understanding modular arithmetic properties.
- Diophantine Equations: These are equations where the solutions are restricted to integers. GCF is crucial in determining the solvability of certain types of Diophantine equations.
- Abstract Algebra: The concept of GCF extends to more abstract mathematical structures, such as rings and ideals.
Conclusion: The Significance of GCF
The seemingly simple task of finding the greatest common factor of 21 and 40, which we found to be 1, opens up a world of mathematical concepts and applications. From simplifying fractions to its fundamental role in advanced mathematical fields, understanding GCF is essential for anyone interested in mathematics and its applications in diverse areas like computer science and cryptography. The methods presented – listing factors, prime factorization, and the Euclidean algorithm – provide versatile tools for tackling GCF calculations, with the Euclidean algorithm proving particularly efficient for larger numbers. The relationship between GCF and LCM further enriches our understanding of number theory, highlighting the interconnectedness of mathematical concepts. Mastering GCF lays a strong groundwork for exploring more complex mathematical concepts and their practical applications.
Latest Posts
Latest Posts
-
How Many Square Miles In A Square Kilometer
May 10, 2025
-
Como Hallar La Distancia Entre Dos Puntos
May 10, 2025
-
Convert Mg L To Mg Ml
May 10, 2025
-
6 7 Km Is How Many Miles
May 10, 2025
-
Good Uv Index To Get Tan
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 21 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.