What Is The Greatest Common Factor Of 24 And 33
Treneri
May 12, 2025 · 5 min read
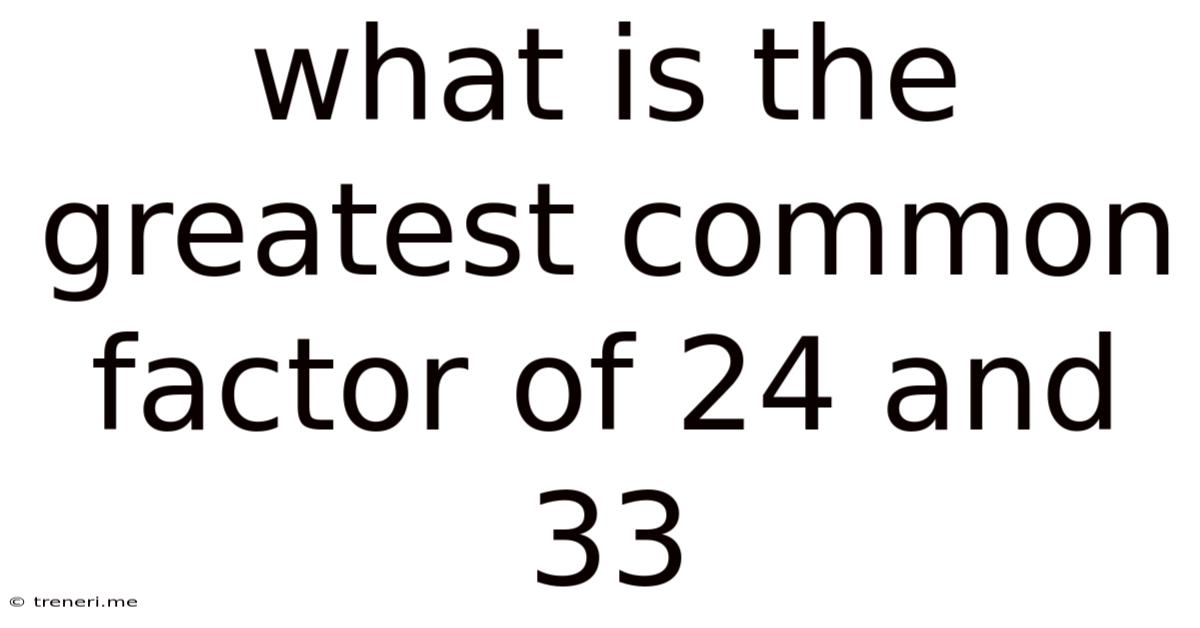
Table of Contents
What is the Greatest Common Factor of 24 and 33? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles reveals a fascinating glimpse into number theory. This article will not only answer the question of the GCF of 24 and 33 but will also explore various methods for finding the GCF, delve into the significance of this concept in mathematics, and highlight its practical applications.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. It's a fundamental concept in number theory that underpins many other mathematical ideas. Think of it as the largest number that perfectly divides both numbers.
For instance, let's consider the factors of 12 and 18:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 18 is 6.
Finding the GCF of 24 and 33: Methods and Solutions
Now, let's address the central question: What is the greatest common factor of 24 and 33? We can employ several methods to determine this:
1. Listing Factors Method
This is a straightforward approach, particularly useful for smaller numbers. We list all the factors of each number and identify the largest factor common to both.
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 33: 1, 3, 11, 33
The common factors are 1 and 3. Therefore, the GCF of 24 and 33 is 3.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 24: 2³ × 3
- Prime factorization of 33: 3 × 11
The only common prime factor is 3, and it appears to the first power in both factorizations. Hence, the GCF of 24 and 33 is 3.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially for larger numbers where listing factors becomes cumbersome. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 24 and 33:
- 33 - 24 = 9 (Now find the GCF of 24 and 9)
- 24 - 9 = 15 (Now find the GCF of 9 and 15)
- 15 - 9 = 6 (Now find the GCF of 9 and 6)
- 9 - 6 = 3 (Now find the GCF of 6 and 3)
- 6 - 3 = 3 (Now find the GCF of 3 and 3)
Since both numbers are now 3, the GCF of 24 and 33 is 3.
Significance of GCF in Mathematics
The GCF plays a crucial role in various areas of mathematics, including:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 24/33 can be simplified by dividing both the numerator and denominator by their GCF, which is 3, resulting in the simplified fraction 8/11.
-
Solving Diophantine Equations: Diophantine equations are algebraic equations where only integer solutions are sought. The GCF is often involved in determining the existence and nature of solutions to these equations.
-
Modular Arithmetic: Modular arithmetic deals with remainders after division. The GCF is crucial in understanding congruence relations and solving modular equations.
-
Number Theory: The GCF is a fundamental concept in number theory, forming the basis for many advanced theorems and concepts.
Practical Applications of GCF
Beyond the purely mathematical realm, the GCF has several practical applications:
-
Dividing Objects: If you have 24 apples and 33 oranges, and you want to divide them into equally sized groups without any leftovers, the GCF (3) tells you the maximum number of groups you can make. Each group would have 8 apples and 11 oranges.
-
Measurement and Construction: In construction or design, the GCF can help determine the largest possible square tiles that can be used to perfectly cover a rectangular area.
-
Resource Allocation: The GCF can be useful in situations where resources need to be divided equally among several groups, ensuring no wastage.
-
Cryptography: While seemingly unrelated, the concept of GCF finds application in certain cryptographic algorithms where the ability to find the GCF of large numbers is critical.
Beyond the Basics: Exploring Related Concepts
Understanding the GCF opens the door to exploring related concepts in number theory:
-
Least Common Multiple (LCM): The least common multiple (LCM) is the smallest positive integer that is a multiple of two or more integers. The GCF and LCM are closely related; for two numbers a and b, their product (a x b) equals the product of their GCF and LCM. (GCF(a,b) x LCM(a,b) = a x b).
-
Coprime Numbers: Two numbers are coprime (or relatively prime) if their GCF is 1. This means they share no common factors other than 1.
-
Euclidean Algorithm Variations: The Euclidean algorithm has various extensions and optimizations, making it an extremely efficient tool for finding the GCF of very large numbers.
Conclusion: The Enduring Importance of the GCF
The greatest common factor, although seemingly a simple concept, holds a significant place in mathematics and various practical applications. Understanding how to find the GCF using different methods—from listing factors to employing the efficient Euclidean algorithm—provides a solid foundation for further exploration of number theory and its applications. The GCF of 24 and 33, determined to be 3, serves as a starting point for appreciating the depth and significance of this fundamental mathematical concept. Its implications extend far beyond simple arithmetic problems, impacting fields ranging from fraction simplification to sophisticated cryptographic techniques. Therefore, mastering the concept of GCF isn't merely about finding a common factor; it's about understanding the building blocks of number theory and its diverse applications in the world around us.
Latest Posts
Latest Posts
-
How To Convert From Grams To Moles In Chemistry
May 12, 2025
-
Uv Index How Long To Burn
May 12, 2025
-
114 Divided By 19 With Remainder
May 12, 2025
-
What Is The Gcf Of 12 And 27
May 12, 2025
-
What Is 9 10 As A Grade
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 24 And 33 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.