What Is The Greatest Common Factor Of 26 And 34
Treneri
May 10, 2025 · 5 min read
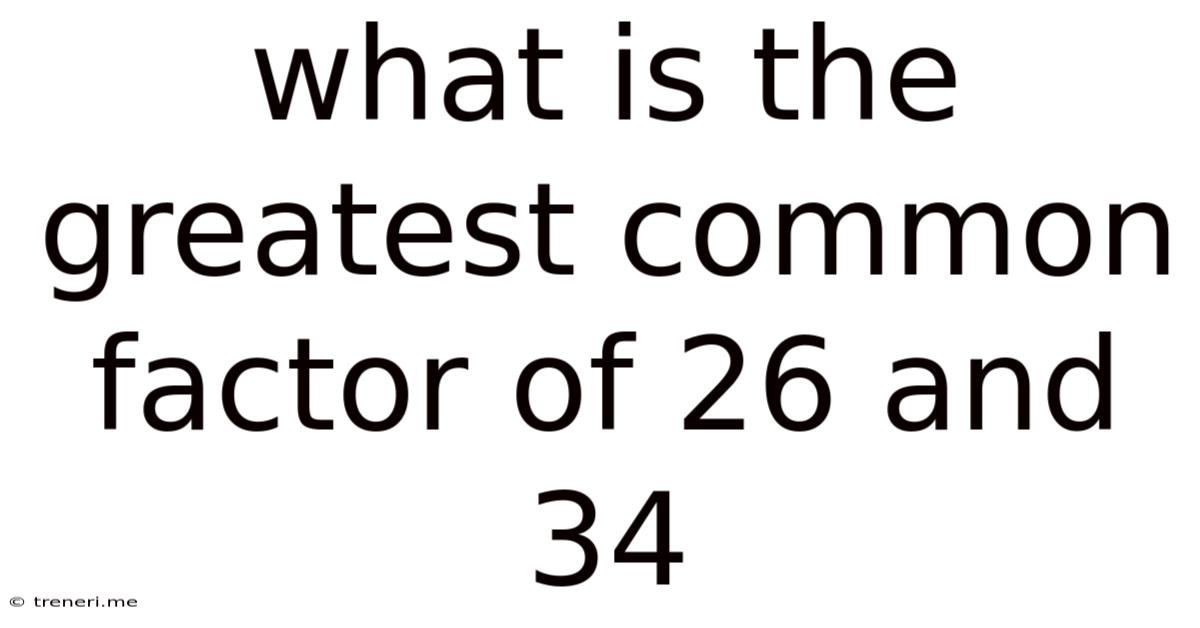
Table of Contents
What is the Greatest Common Factor of 26 and 34? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and various methods can be surprisingly insightful. This article delves into determining the GCF of 26 and 34, exploring multiple approaches and highlighting their practical applications in mathematics and beyond. We'll move beyond a simple answer to provide a comprehensive understanding of this fundamental concept.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. This concept is crucial in various mathematical operations, from simplifying fractions to solving algebraic equations.
Why is finding the GCF important?
The GCF has numerous applications:
- Simplifying Fractions: Reducing fractions to their simplest form requires finding the GCF of the numerator and denominator.
- Algebraic Expressions: Factoring algebraic expressions often involves finding the GCF of the terms.
- Problem Solving: Many real-world problems, particularly those involving division and distribution, benefit from finding the GCF.
- Number Theory: GCF is a fundamental concept in number theory, forming the basis for more advanced topics.
Methods for Finding the GCF of 26 and 34
Several methods can be used to determine the GCF of 26 and 34. Let's explore the most common ones:
1. Listing Factors Method
This is a straightforward method, especially for smaller numbers. We list all the factors of each number and identify the largest common factor.
Factors of 26: 1, 2, 13, 26 Factors of 34: 1, 2, 17, 34
Comparing the two lists, we see that the common factors are 1 and 2. The greatest of these is 2.
Therefore, the GCF of 26 and 34 is 2.
2. Prime Factorization Method
This method uses the prime factorization of each number. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Prime Factorization of 26: 2 x 13 Prime Factorization of 34: 2 x 17
The common prime factor is 2. Therefore, the GCF is 2. This method is particularly useful for larger numbers where listing factors becomes cumbersome.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is the GCF.
Let's apply the Euclidean algorithm to 26 and 34:
- 34 - 26 = 8 (Now we find the GCF of 26 and 8)
- 26 - 8 = 18 (Now we find the GCF of 8 and 18)
- 18 - 8 = 10 (Now we find the GCF of 8 and 10)
- 10 - 8 = 2 (Now we find the GCF of 8 and 2)
- 8 - 2 = 6 (Now we find the GCF of 2 and 6)
- 6 - 2 = 4 (Now we find the GCF of 2 and 4)
- 4 - 2 = 2 (Now we find the GCF of 2 and 2)
Since both numbers are now 2, the GCF of 26 and 34 is 2.
Applications of GCF in Real-World Scenarios
The concept of GCF extends beyond abstract mathematical problems and finds practical applications in various real-world situations:
-
Dividing Items into Equal Groups: Imagine you have 26 apples and 34 oranges. You want to divide them into equal groups, with the same number of apples and oranges in each group. The GCF (2) tells you can create 2 groups, each with 13 apples and 17 oranges.
-
Simplifying Recipes: Suppose a recipe calls for 26 cups of flour and 34 cups of sugar. To simplify the recipe for a smaller batch, you can divide both quantities by their GCF (2), resulting in a recipe that requires 13 cups of flour and 17 cups of sugar.
-
Tiling and Construction: In tiling or construction projects, determining the largest square tile that can be used to cover a rectangular area evenly involves finding the GCF of the dimensions of the rectangle.
Advanced Concepts Related to GCF
The GCF is a stepping stone to more advanced mathematical concepts:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of two or more numbers. The GCF and LCM are related by the formula: GCF(a, b) * LCM(a, b) = a * b.
-
Modular Arithmetic: GCF plays a critical role in modular arithmetic, which deals with remainders after division.
-
Diophantine Equations: These equations involve finding integer solutions, and GCF is often used in solving them.
Conclusion: The Power of the GCF
The seemingly simple task of finding the greatest common factor reveals a surprisingly rich mathematical concept with wide-ranging applications. Whether using the straightforward listing method, the elegant prime factorization approach, or the efficient Euclidean algorithm, understanding how to find the GCF empowers you to solve problems in various mathematical contexts and real-world situations. Beyond the calculation itself, the understanding of prime numbers, factorization, and the relationships between numbers provides a strong foundation for more advanced mathematical explorations. The GCF is not just a number; it’s a key that unlocks a deeper appreciation for the structure and beauty of mathematics. Remember, the GCF of 26 and 34 is definitively 2, and understanding the how and why behind this calculation provides invaluable insight into the broader world of mathematics.
Latest Posts
Latest Posts
-
19 Sq Meters To Sq Ft
May 10, 2025
-
1 8 Per Foot Slope In Percent
May 10, 2025
-
5 Is 1 Of What Number
May 10, 2025
-
What Is The Measure Of 44 50 64 92
May 10, 2025
-
How Many Days Is In Two Months
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 26 And 34 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.