What Is The Greatest Common Factor Of 32 And 48
Treneri
May 11, 2025 · 5 min read
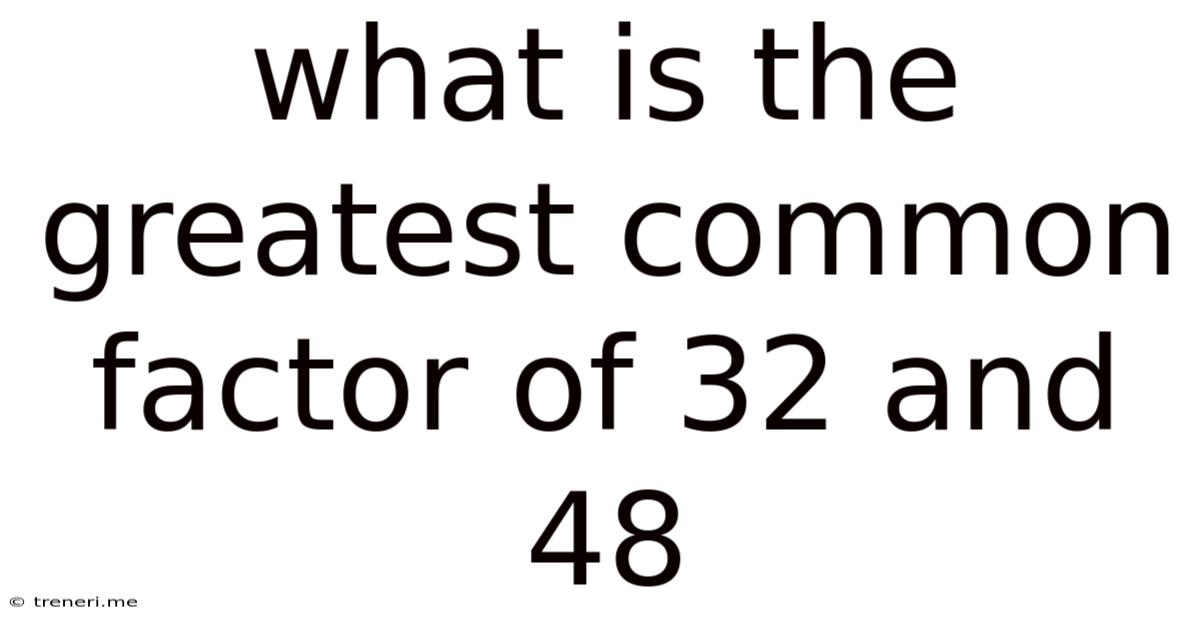
Table of Contents
What is the Greatest Common Factor of 32 and 48? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and different methods involved opens the door to a deeper appreciation of number theory and its applications. This article will explore various ways to determine the GCF of 32 and 48, delve into the theoretical foundation of GCFs, and demonstrate their practical relevance in various mathematical contexts.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For example, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 evenly.
Understanding the concept of GCF is crucial for simplifying fractions, solving algebraic equations, and tackling more advanced mathematical problems. It forms the bedrock of many fundamental mathematical operations and is frequently applied in various fields, including computer science and cryptography.
Method 1: Listing Factors
The most straightforward method to find the GCF is by listing all the factors of each number and then identifying the largest factor common to both.
Factors of 32: 1, 2, 4, 8, 16, 32 Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Comparing the two lists, we can see that the common factors are 1, 2, 4, 8, and 16. The greatest common factor is 16.
Method 2: Prime Factorization
Prime factorization involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. This method is particularly useful for larger numbers where listing factors might become cumbersome.
Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup> Prime factorization of 48: 2 x 2 x 2 x 2 x 3 = 2<sup>4</sup> x 3
To find the GCF using prime factorization, we identify the common prime factors and multiply them together, raising each to the lowest power it appears in either factorization. In this case, the only common prime factor is 2, and the lowest power it appears is 2<sup>4</sup>.
Therefore, the GCF of 32 and 48 is 2<sup>4</sup> = 16.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is then the GCF.
Let's apply the Euclidean algorithm to 32 and 48:
- 48 - 32 = 16
- 32 - 16 = 16
Since both numbers are now 16, the GCF of 32 and 48 is 16. This method is significantly more efficient than listing factors or prime factorization when dealing with large numbers.
The Significance of the Greatest Common Factor
The GCF has numerous applications across various mathematical domains and beyond:
-
Simplifying Fractions: The GCF is fundamental in simplifying fractions to their lowest terms. For instance, the fraction 32/48 can be simplified by dividing both the numerator and the denominator by their GCF (16), resulting in the simplified fraction 2/3.
-
Solving Equations: GCF plays a crucial role in solving algebraic equations, particularly those involving polynomials. Factoring out the GCF helps simplify expressions and find solutions more easily.
-
Number Theory: GCF is a cornerstone concept in number theory, used in topics like modular arithmetic, cryptography, and the study of Diophantine equations (equations involving integers).
-
Geometry and Measurement: GCF is essential in solving geometrical problems involving area calculations, finding the side lengths of similar figures, and dealing with measurements and units.
-
Computer Science: The Euclidean algorithm, used to find the GCF, is a fundamental algorithm in computer science, optimized for its efficiency in handling large numbers. Its applications extend to cryptography, particularly in public-key cryptography systems.
Beyond 32 and 48: Generalizing the GCF
The methods described above for finding the GCF of 32 and 48 are applicable to any pair of integers. Whether using listing factors, prime factorization, or the Euclidean algorithm, the core principle remains the same: identifying the largest integer that divides both numbers without leaving a remainder.
The choice of method often depends on the size of the numbers. For small numbers, listing factors might be sufficient. For larger numbers, the Euclidean algorithm provides a significantly more efficient approach. Prime factorization offers a theoretical understanding and is valuable in more advanced mathematical contexts.
Practical Applications and Real-World Examples
The GCF isn't just a theoretical concept; it has tangible applications in various real-world scenarios:
-
Dividing Resources: Imagine you have 32 apples and 48 oranges, and you want to divide them equally among groups of people such that each group receives the same number of apples and oranges. The GCF (16) represents the maximum number of groups you can form while ensuring each group gets a whole number of both apples and oranges.
-
Arranging Objects: Suppose you're arranging 32 square tiles and 48 rectangular tiles into identical square formations. The GCF (16) indicates the largest number of identical formations you can create using all the tiles without any leftover.
-
Manufacturing and Production: In manufacturing, GCF is helpful in determining the size of the largest identical parts that can be cut from larger sheets of material, minimizing waste.
Conclusion: Mastering the GCF
Understanding the greatest common factor goes beyond simple arithmetic. It’s a foundational concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex equations and optimizing real-world problems. By mastering the various methods of finding the GCF – listing factors, prime factorization, and the Euclidean algorithm – you equip yourself with a powerful tool for tackling diverse mathematical challenges and enhancing your problem-solving skills across various disciplines. The simple question of "What is the greatest common factor of 32 and 48?" thus becomes a gateway to a deeper understanding of number theory and its practical significance. Remember that consistent practice with these methods is key to solidifying your understanding and improving your efficiency in finding the GCF for any pair of integers.
Latest Posts
Latest Posts
-
What Is A 4 12 Pitch Roof
May 12, 2025
-
How Many Days Until Next Monday
May 12, 2025
-
How Much Popcorn Does 1 2 Cup Make
May 12, 2025
-
How Many Years Is 2000 Months
May 12, 2025
-
How Big Is A 9000 Square Foot Lot
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 32 And 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.