What Is The Greatest Common Factor Of 32 And 64
Treneri
May 10, 2025 · 5 min read
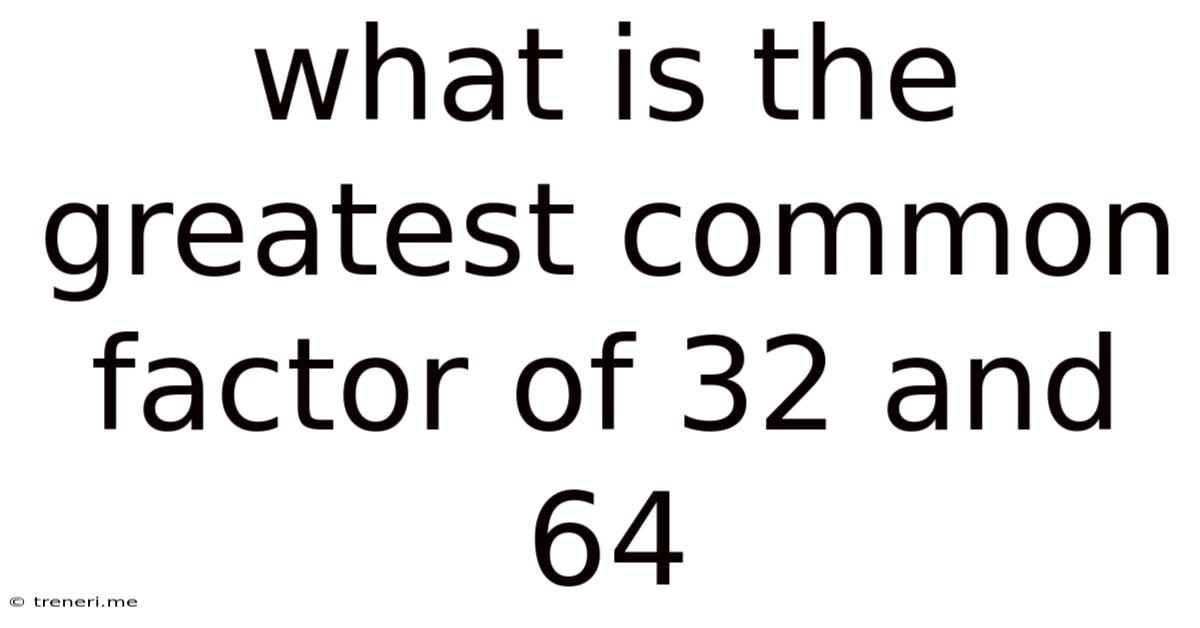
Table of Contents
What is the Greatest Common Factor of 32 and 64? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles reveals a fascinating connection to number theory and its applications in various fields. This article delves into the intricacies of finding the GCF of 32 and 64, exploring multiple methods and expanding upon the broader significance of this concept. We'll go beyond simply stating the answer; we'll explore why the answer is what it is and how this knowledge extends to more complex mathematical scenarios.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers perfectly. This concept is fundamental in simplifying fractions, solving algebraic equations, and even in advanced areas like cryptography.
Why is Finding the GCF Important?
The GCF has practical applications in various aspects of mathematics and beyond:
-
Simplifying Fractions: Reducing fractions to their simplest form relies heavily on finding the GCF of the numerator and denominator. For example, simplifying 64/32 requires finding the GCF, which allows for efficient simplification.
-
Algebraic Simplification: Factoring algebraic expressions often involves finding the GCF of the terms to simplify the expression.
-
Geometry: Determining the dimensions of the largest square tile that can perfectly cover a rectangular area involves finding the GCF of the rectangle's length and width.
-
Cryptography: Concepts related to GCF, such as the Euclidean algorithm, play a crucial role in modern encryption techniques.
Methods for Finding the GCF of 32 and 64
Let's explore different ways to determine the GCF of 32 and 64:
1. Listing Factors
The most straightforward method is listing all the factors of each number and identifying the largest common factor.
- Factors of 32: 1, 2, 4, 8, 16, 32
- Factors of 64: 1, 2, 4, 8, 16, 32, 64
By comparing the two lists, we observe that the largest common factor is 32.
2. Prime Factorization
This method involves expressing each number as a product of its prime factors. The GCF is then the product of the common prime factors raised to the lowest power.
- Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
- Prime factorization of 64: 2 x 2 x 2 x 2 x 2 x 2 = 2<sup>6</sup>
Both numbers share five factors of 2. Therefore, the GCF is 2<sup>5</sup> = 32.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, which is the GCF.
Let's apply the Euclidean algorithm to 32 and 64:
- 64 = 32 x 2 + 0
Since the remainder is 0, the GCF is the smaller number, which is 32.
Expanding the Concept: GCF and LCM
The greatest common factor (GCF) is closely related to the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of both numbers. There's a crucial relationship between the GCF and LCM of two numbers:
GCF(a, b) x LCM(a, b) = a x b
For our example:
- GCF(32, 64) = 32
- LCM(32, 64) = 64
Let's verify the relationship:
32 x 64 = 2048 32 x 64 = 2048
The equation holds true, demonstrating the connection between GCF and LCM.
Applications Beyond Basic Arithmetic
The concept of GCF extends far beyond simple arithmetic problems. Its significance spans various fields:
1. Computer Science and Cryptography
The Euclidean algorithm, used to find the GCF, is a cornerstone of many cryptographic algorithms. It's essential for tasks like key generation and secure communication.
2. Music Theory
The GCF plays a role in understanding musical intervals and harmonies. The GCF of two frequencies determines the simplest ratio between them, influencing the perceived consonance or dissonance of the notes.
3. Geometry and Measurement
Determining the size of the largest square tile that can perfectly cover a rectangular area involves finding the GCF of the rectangle's length and width. This concept is used in tiling problems, architectural design, and various other applications.
4. Data Analysis and Statistics
In data analysis, the GCF can be useful in simplifying data sets or identifying patterns. For instance, when dealing with data points that are multiples of a certain number, finding the GCF can help streamline the analysis.
Conclusion: The Power of a Simple Concept
While finding the greatest common factor of 32 and 64 might seem trivial at first glance, the underlying principles and its wider applications demonstrate the profound influence of this seemingly simple concept in various fields. From simplifying fractions to securing online transactions, the GCF is a fundamental building block of mathematics and its applications in the modern world. Understanding the different methods for calculating the GCF, such as the listing factors, prime factorization, and Euclidean algorithm, provides a comprehensive understanding of this vital mathematical concept and its pervasive role in numerous disciplines. The connection between the GCF and the LCM further enriches our understanding of number theory and its implications. Therefore, mastering the GCF is not just about solving arithmetic problems; it's about grasping a fundamental concept that underpins numerous advanced mathematical and computational processes.
Latest Posts
Latest Posts
-
Cuanto Es 111 Libras En Kilos
May 11, 2025
-
How Many Hours Is 11 30 To 7
May 11, 2025
-
How Much Is 150 Ml In Oz
May 11, 2025
-
What Is 15327 Rounded To The Nearest Ten Thousand
May 11, 2025
-
Gigabit Per Second To Gigabyte Per Second
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 32 And 64 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.