What Is The Greatest Common Factor Of 32 And 80
Treneri
May 14, 2025 · 5 min read
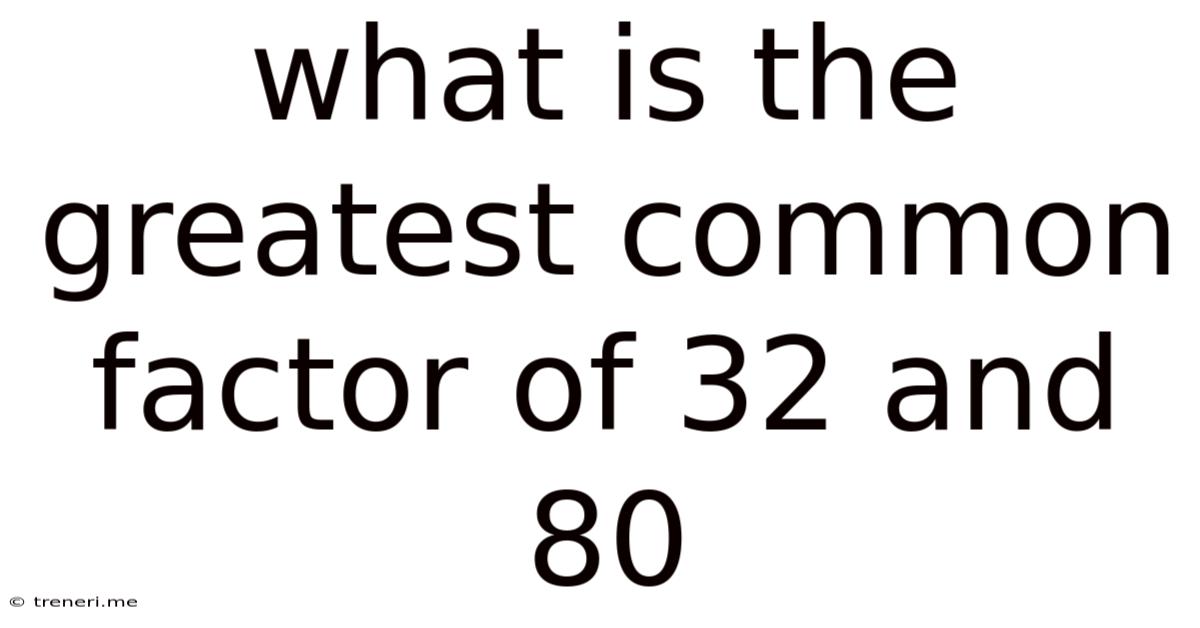
Table of Contents
What is the Greatest Common Factor of 32 and 80? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with applications far beyond basic math. This article will not only answer the question of what the GCF of 32 and 80 is, but will explore multiple methods for finding the GCF, discuss its significance in mathematics, and delve into related concepts.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and understanding more advanced mathematical concepts.
Methods for Finding the GCF of 32 and 80
Several methods exist to determine the GCF of 32 and 80. Let's explore the most common approaches:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to both.
- Factors of 32: 1, 2, 4, 8, 16, 32
- Factors of 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Comparing the two lists, we see that the common factors are 1, 2, 4, 8, and 16. The greatest common factor is therefore 16.
This method works well for smaller numbers, but becomes cumbersome for larger numbers with many factors.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2⁵
- Prime factorization of 80: 2 x 2 x 2 x 2 x 5 = 2⁴ x 5
The common prime factor is 2, and the lowest power is 2⁴. Therefore, the GCF is 2⁴ = 16.
This method is more efficient for larger numbers as it systematically breaks down the numbers into their prime components.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly for larger numbers. It's based on repeated application of the division algorithm.
- Divide the larger number (80) by the smaller number (32): 80 ÷ 32 = 2 with a remainder of 16.
- Replace the larger number with the smaller number (32) and the smaller number with the remainder (16): 32 ÷ 16 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 16.
The Euclidean algorithm is efficient because it avoids the need to list all factors, making it suitable for large numbers where the listing method becomes impractical.
The Significance of GCF
The GCF is not just a mathematical curiosity; it has significant applications in various areas:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 80/32 can be simplified by dividing both the numerator and denominator by their GCF (16), resulting in the simplified fraction 5/2.
-
Solving Algebraic Equations: GCF plays a vital role in factoring algebraic expressions. Factoring allows us to simplify expressions and solve equations more easily.
-
Geometry and Measurement: GCF is essential in solving problems related to area, perimeter, and volume. For instance, finding the largest square tile that can perfectly cover a rectangular floor requires calculating the GCF of the floor's dimensions.
-
Number Theory: GCF is a fundamental concept in number theory, forming the basis for other concepts like least common multiple (LCM) and modular arithmetic. Understanding GCF is key to understanding more advanced concepts in number theory.
Least Common Multiple (LCM) and its Relationship with GCF
The least common multiple (LCM) is the smallest positive integer that is a multiple of each of the integers. The LCM and GCF are closely related. For any two positive integers a and b, the product of their GCF and LCM is equal to the product of the two numbers:
GCF(a, b) * LCM(a, b) = a * b
Therefore, if we know the GCF of 32 and 80 (which is 16), we can calculate the LCM:
LCM(32, 80) = (32 * 80) / GCF(32, 80) = (32 * 80) / 16 = 160
This relationship provides a convenient way to find the LCM if the GCF is already known.
Applications of GCF and LCM in Real-World Scenarios
The concepts of GCF and LCM extend beyond abstract mathematical exercises. They find practical applications in various real-world situations:
-
Scheduling: Imagine two buses that depart from the same station at different intervals. Finding the LCM of their departure intervals helps determine when they will depart at the same time again.
-
Construction and Design: In construction, GCF and LCM are used in determining optimal dimensions for materials, ensuring efficient use of resources.
-
Music Theory: Musical intervals and harmonies are related to the LCM and GCF of frequencies.
-
Computer Science: GCF and LCM algorithms are used in various computational tasks such as cryptography and data compression.
Advanced Concepts Related to GCF
The study of GCF leads to more advanced concepts in number theory, including:
-
Modular Arithmetic: GCF is crucial in understanding modular arithmetic, which forms the basis for cryptography and other computational applications.
-
Diophantine Equations: GCF is essential in solving Diophantine equations, which are equations involving only integers.
-
Abstract Algebra: The concept of GCF generalizes to more abstract mathematical structures such as rings and ideals, where the concept is referred to as greatest common divisor.
Conclusion: The Power of a Simple Concept
While finding the GCF of 32 and 80 might appear to be a simple exercise, it reveals a profound concept with far-reaching implications in mathematics and beyond. Understanding the different methods for calculating GCF and its relationship to LCM empowers us to solve a wide array of problems, from simplifying fractions to understanding complex number theory. The seemingly basic concept of the greatest common factor unveils a powerful tool with applications that extend far beyond the classroom. Its importance in various fields underscores its significance as a fundamental building block of mathematics and its practical application in the real world.
Latest Posts
Latest Posts
-
How Many Days Left Of September
May 15, 2025
-
How To Find Board Feet In A Log
May 15, 2025
-
22 Out Of 30 As A Percentage Grade
May 15, 2025
-
Convert 3 4 Cup To Ounces
May 15, 2025
-
How Many Ounces Is 45 G
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 32 And 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.