What Is The Greatest Common Factor Of 36 And 81
Treneri
May 12, 2025 · 5 min read
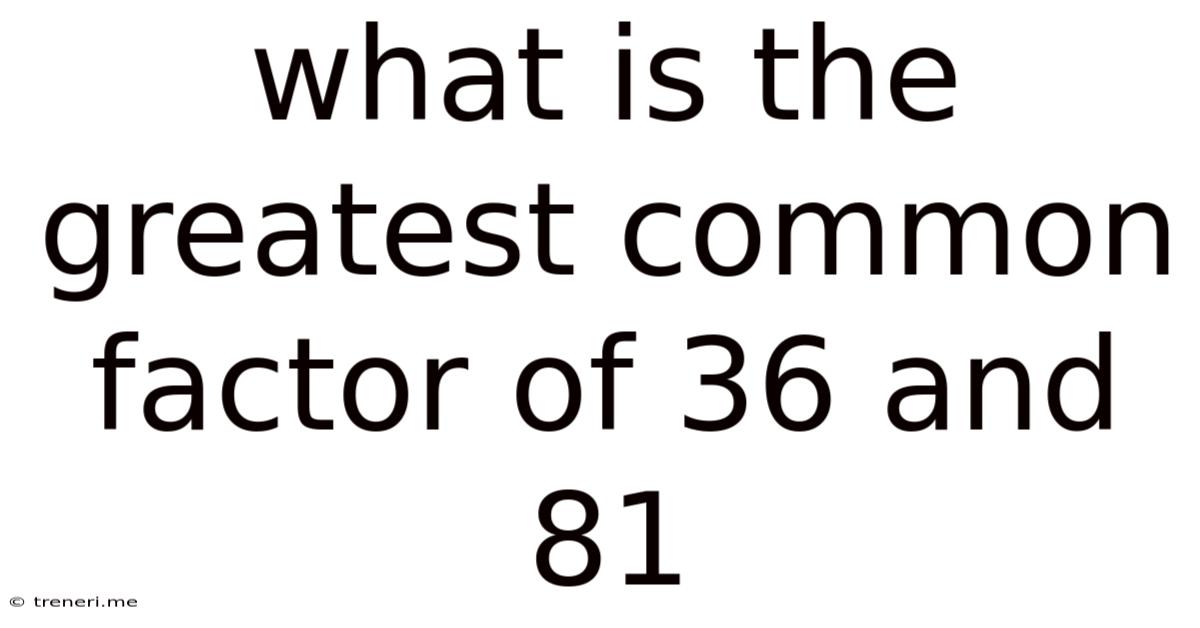
Table of Contents
What is the Greatest Common Factor of 36 and 81? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a concept with surprisingly deep roots in number theory and a wide range of applications in mathematics and beyond. This article will explore the GCF of 36 and 81, demonstrating multiple methods for finding it, and then delve into the broader significance of this fundamental mathematical idea.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. Understanding the GCF is crucial for simplifying fractions, solving algebraic equations, and numerous other mathematical operations.
Methods for Finding the GCF of 36 and 81
There are several effective methods to determine the GCF of 36 and 81. Let's examine three common approaches:
1. Prime Factorization Method
This method involves breaking down each number into its prime factors – the prime numbers that multiply together to make the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 36: 2 x 2 x 3 x 3 = 2² x 3²
- Prime factorization of 81: 3 x 3 x 3 x 3 = 3⁴
To find the GCF, we identify the common prime factors and their lowest powers. Both 36 and 81 share the prime factor 3. The lowest power of 3 present in both factorizations is 3².
Therefore, the GCF(36, 81) = 3² = 9
2. Listing Factors Method
This method involves listing all the factors (divisors) of each number and then identifying the largest factor common to both lists.
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
- Factors of 81: 1, 3, 9, 27, 81
Comparing the two lists, we find that the common factors are 1, 3, and 9. The largest of these common factors is 9.
Therefore, the GCF(36, 81) = 9
3. Euclidean Algorithm Method
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 36 and 81:
- 81 = 2 x 36 + 9
- 36 = 4 x 9 + 0
Since the remainder is 0, the GCF is the last non-zero remainder, which is 9.
Therefore, the GCF(36, 81) = 9
Applications of the Greatest Common Factor
The GCF has numerous practical applications across various fields:
1. Simplifying Fractions
The GCF plays a vital role in simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, the fraction 36/81 can be simplified by dividing both the numerator and the denominator by their GCF, which is 9:
36/81 = (36 ÷ 9) / (81 ÷ 9) = 4/9
2. Solving Algebraic Equations
The GCF is frequently used in factoring algebraic expressions. Factoring involves expressing an algebraic expression as a product of simpler expressions. Finding the GCF of the terms in an expression allows for simplification and solving equations more easily.
3. Geometry and Measurement
The GCF is useful in solving geometric problems related to area and perimeter calculations. For instance, when dividing a rectangular area into smaller squares of equal size, the side length of the squares must be a common factor of the rectangle's length and width. The largest possible square size would be determined by the GCF of the length and width.
4. Number Theory and Cryptography
The GCF is a fundamental concept in number theory, with significant applications in cryptography. Algorithms like the Euclidean algorithm are used in modern cryptography for tasks such as key generation and encryption/decryption processes.
5. Real-World Applications
Beyond theoretical mathematics, the GCF finds practical applications in everyday life:
- Dividing items equally: When sharing items among a group of people, the GCF helps determine the largest equal number of items each person can receive.
- Arranging objects in arrays: The GCF can help determine the maximum number of rows and columns when arranging objects into a rectangular array.
- Scheduling tasks: In project management, the GCF can help find the optimal time intervals for repeating tasks.
Beyond the Basics: Exploring Related Concepts
Understanding the GCF opens doors to exploring related concepts in number theory:
- Least Common Multiple (LCM): The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. The GCF and LCM are related by the formula: GCF(a, b) x LCM(a, b) = a x b.
- Coprime Numbers: Two numbers are coprime (or relatively prime) if their GCF is 1.
- Modular Arithmetic: The GCF plays a significant role in modular arithmetic, which deals with remainders after division.
Conclusion: The Enduring Importance of the GCF
The seemingly simple task of finding the greatest common factor of 36 and 81 reveals a much deeper mathematical concept with extensive applications across various fields. From simplifying fractions to securing cryptographic systems, the GCF serves as a fundamental building block in mathematics and its practical applications. Mastering the techniques for finding the GCF not only strengthens arithmetic skills but also provides a foundation for understanding more advanced mathematical concepts. The methods discussed – prime factorization, listing factors, and the Euclidean algorithm – provide diverse approaches to tackle this important problem, highlighting the rich and interconnected nature of number theory. Understanding the GCF is not just about finding a single answer; it's about unlocking a deeper appreciation for the elegance and power of mathematical principles.
Latest Posts
Latest Posts
-
Can A Right Triangle Be Both Scalene And Isosceles
May 12, 2025
-
How Much Is 50000 Miles Worth
May 12, 2025
-
Born April 1978 How Old Am I
May 12, 2025
-
2 3 8 1 1 4
May 12, 2025
-
Cuanto Es 1 5 Kg En Libras
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 36 And 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.