What Is The Greatest Common Factor Of 39 And 52
Treneri
May 10, 2025 · 5 min read
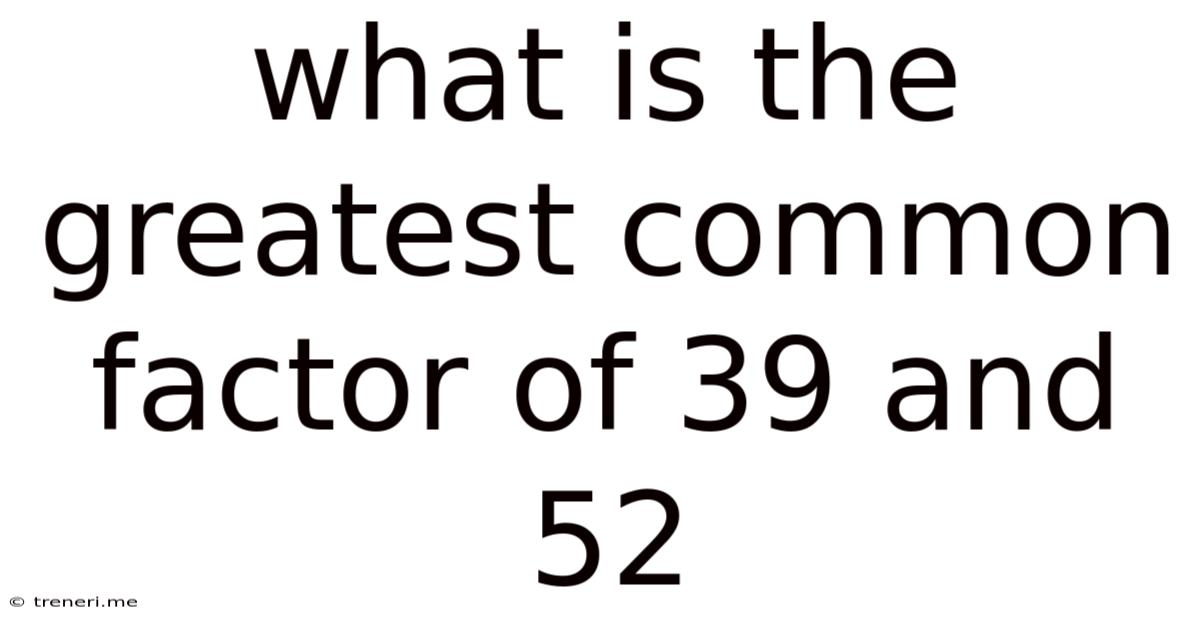
Table of Contents
What is the Greatest Common Factor of 39 and 52? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and different methods for calculating it unlocks a deeper appreciation for number theory and its applications. This article will explore various ways to determine the GCF of 39 and 52, going beyond a simple answer to delve into the theory and practical uses of this fundamental concept in mathematics.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into both numbers. Understanding this concept is crucial for simplifying fractions, solving algebraic equations, and even in more advanced mathematical fields.
Why is finding the GCF important?
The GCF has numerous applications across various mathematical domains:
- Simplifying Fractions: Reducing fractions to their simplest form requires finding the GCF of the numerator and denominator. For example, simplifying 12/18 requires finding the GCF of 12 and 18 (which is 6), resulting in the simplified fraction 2/3.
- Solving Algebraic Equations: The GCF plays a crucial role in factoring polynomials, a fundamental technique in algebra. Factoring allows for simplifying complex equations and solving them more easily.
- Number Theory: The GCF is a core concept in number theory, which explores the properties of integers. Advanced concepts like modular arithmetic and cryptography rely heavily on understanding GCFs.
- Real-World Applications: From dividing resources fairly to designing efficient structures, the principles of GCF find practical applications in various real-world scenarios.
Method 1: Prime Factorization
The prime factorization method is a systematic approach to finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Finding the Prime Factors of 39:
39 is not divisible by 2. 39 is divisible by 3 (39/3 = 13). 13 is a prime number.
Therefore, the prime factorization of 39 is 3 x 13.
Finding the Prime Factors of 52:
52 is divisible by 2 (52/2 = 26). 26 is divisible by 2 (26/2 = 13). 13 is a prime number.
Therefore, the prime factorization of 52 is 2 x 2 x 13, or 2² x 13.
Determining the GCF using Prime Factorization:
Now, we compare the prime factorizations of 39 and 52:
39 = 3 x 13 52 = 2² x 13
The common prime factor is 13. Since it's the only common factor, the greatest common factor of 39 and 52 is 13.
Method 2: Listing Factors
This method involves listing all the factors of each number and identifying the largest common factor. While simpler for smaller numbers, it becomes less efficient with larger numbers.
Factors of 39:
1, 3, 13, 39
Factors of 52:
1, 2, 4, 13, 26, 52
Identifying the GCF:
Comparing the lists, we see that the common factors are 1 and 13. The largest common factor is 13. Therefore, the GCF of 39 and 52 is 13.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
- Divide the larger number (52) by the smaller number (39): 52 ÷ 39 = 1 with a remainder of 13.
- Replace the larger number with the remainder: The new pair is 39 and 13.
- Repeat the process: 39 ÷ 13 = 3 with a remainder of 0.
- The GCF is the last non-zero remainder: Since the remainder is 0, the GCF is the previous remainder, which is 13.
The Euclidean algorithm provides a concise and efficient way to determine the GCF, especially when dealing with larger numbers where the prime factorization method might become cumbersome.
Applications of GCF: Real-World Examples
The concept of GCF isn't confined to theoretical mathematics; it has practical applications in various real-world scenarios.
-
Dividing Resources: Imagine you have 39 apples and 52 oranges, and you want to divide them into identical groups with the maximum number of groups possible, ensuring each group has the same number of apples and oranges. The GCF (13) determines that you can create 13 identical groups, each with 3 apples and 4 oranges.
-
Geometric Problems: Consider designing a rectangular area using tiles. If you have tiles of size 39 cm x 52 cm, the GCF (13 cm) helps determine the largest square tiles that can perfectly cover the rectangular area without any gaps or overlaps.
-
Simplification of Ratios: In recipes or engineering, simplifying ratios is often necessary. For instance, if a mixture requires a ratio of 39 parts of ingredient A to 52 parts of ingredient B, simplifying this ratio using the GCF (13) results in a simpler ratio of 3:4.
Expanding on the Concept: Least Common Multiple (LCM)
While this article focuses on GCF, it's important to mention the closely related concept of the Least Common Multiple (LCM). The LCM is the smallest positive integer that is a multiple of both numbers. GCF and LCM are interconnected; their product is equal to the product of the original two numbers: GCF(a, b) * LCM(a, b) = a * b. Understanding both GCF and LCM is essential for solving various mathematical problems.
Conclusion: The Power of the GCF
Determining the greatest common factor of 39 and 52, as demonstrated through prime factorization, listing factors, and the Euclidean algorithm, reveals more than just a simple answer (13). It showcases the fundamental principles of number theory and highlights its practical applications in various fields. Whether simplifying fractions, solving algebraic equations, or tackling real-world problems, understanding and applying the GCF is a crucial skill in mathematics and beyond. The different methods presented here offer flexibility depending on the complexity of the numbers involved, emphasizing the versatility and importance of this core mathematical concept. Mastering the GCF opens doors to a deeper understanding of mathematical relationships and their practical implications.
Latest Posts
Latest Posts
-
How Many More Minutes Until 1 30
May 10, 2025
-
What Is The Reciprocal Of 4 9
May 10, 2025
-
Density Of Glass In G Cm3
May 10, 2025
-
Como Calcular Los Galones De Agua De Una Piscina
May 10, 2025
-
60 Days After October 24 2024
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 39 And 52 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.