What Is The Greatest Common Factor Of 4 And 9
Treneri
May 14, 2025 · 5 min read
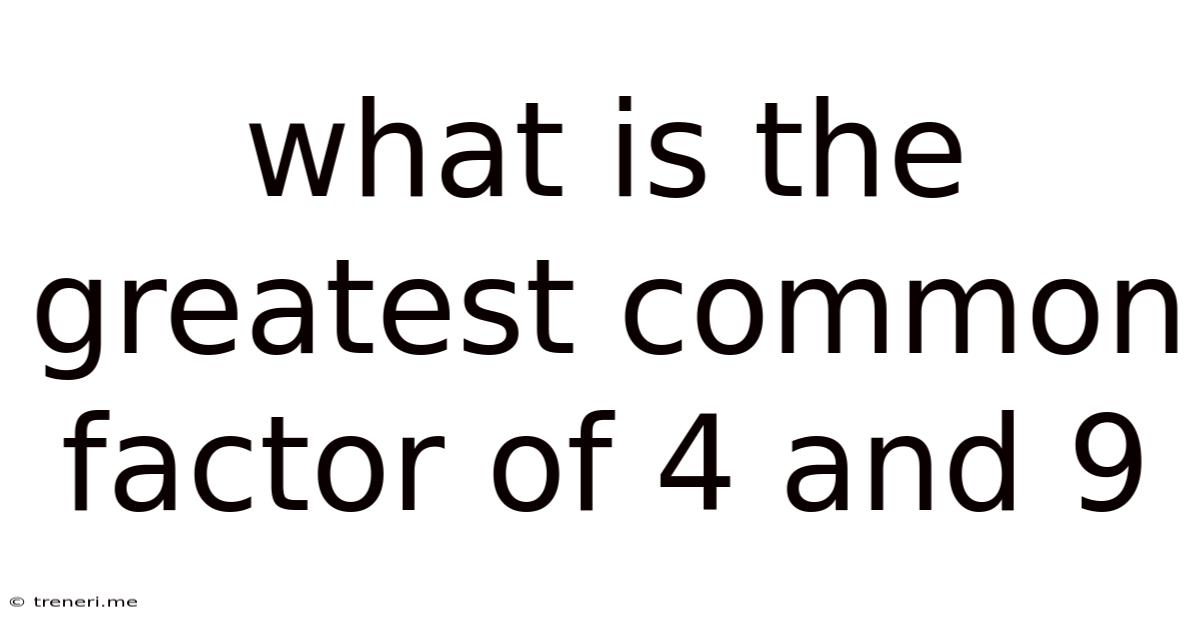
Table of Contents
What is the Greatest Common Factor of 4 and 9? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with applications far beyond basic mathematics. This article delves into the GCF of 4 and 9, exploring different methods for calculating it and highlighting its significance in various mathematical contexts. While the answer itself is straightforward, understanding the underlying principles provides valuable insights into the structure of numbers and their relationships.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. Finding the GCF is a crucial step in simplifying fractions, solving equations, and understanding other number-theoretic concepts.
Why is the GCF Important?
The GCF has numerous applications across various mathematical fields:
-
Fraction Simplification: The GCF is essential for simplifying fractions to their lowest terms. Dividing both the numerator and denominator by their GCF reduces the fraction to its simplest form.
-
Algebraic Expressions: Finding the GCF helps factor algebraic expressions, making them easier to solve or manipulate. This is particularly important in solving polynomial equations.
-
Number Theory: The GCF plays a central role in many number-theoretic concepts, including modular arithmetic, Diophantine equations, and the Euclidean algorithm.
-
Computer Science: Efficient algorithms for finding the GCF are crucial in computer science applications, such as cryptography and computer-aided design.
Calculating the GCF of 4 and 9
Now, let's focus on determining the GCF of 4 and 9. Several methods can be employed:
1. Listing Factors Method
This is a straightforward method, especially for smaller numbers. We list all the factors of each number and identify the largest common factor.
Factors of 4: 1, 2, 4 Factors of 9: 1, 3, 9
The common factors of 4 and 9 are only 1. Therefore, the GCF of 4 and 9 is 1.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and identifying the common prime factors raised to the lowest power.
- Prime factorization of 4: 2²
- Prime factorization of 9: 3²
Since 4 and 9 have no common prime factors, their GCF is 1.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 4 and 9:
- Start with the larger number (9) and the smaller number (4).
- Divide 9 by 4: 9 = 4 × 2 + 1
- Replace 9 with the remainder (1) and repeat the process with 4 and 1.
- Divide 4 by 1: 4 = 1 × 4 + 0
- The remainder is 0, so the GCF is the last non-zero remainder, which is 1.
Significance of the GCF being 1
When the GCF of two numbers is 1, we say that the numbers are relatively prime, coprime, or mutually prime. This means that the numbers share no common factors other than 1. This property has significant implications in various mathematical contexts:
-
Irreducible Fractions: If the numerator and denominator of a fraction are relatively prime, the fraction is in its simplest form and cannot be further reduced. The fraction 4/9 is already in its simplest form because GCF(4,9) = 1.
-
Modular Arithmetic: Relatively prime numbers play a crucial role in modular arithmetic, which is widely used in cryptography and computer science.
-
Number Theory Theorems: Many number theory theorems rely on the concept of relatively prime numbers, further emphasizing their importance in the field.
Exploring Further: GCF and LCM
The greatest common factor (GCF) is closely related to the least common multiple (LCM). The LCM of two or more integers is the smallest positive integer that is a multiple of each of the integers. There's a fundamental relationship between the GCF and LCM:
For any two integers 'a' and 'b', the product of their GCF and LCM is equal to the product of the two numbers:
GCF(a, b) × LCM(a, b) = a × b
Using this relationship, we can calculate the LCM of 4 and 9:
GCF(4, 9) × LCM(4, 9) = 4 × 9 1 × LCM(4, 9) = 36 LCM(4, 9) = 36
Therefore, the least common multiple of 4 and 9 is 36.
Applications in Real-World Scenarios
While the concept of the GCF might seem abstract, it has practical applications in various real-world situations:
-
Dividing Resources: Imagine you have 4 apples and 9 oranges, and you want to divide them equally among several people without having any leftovers. The GCF (1) indicates that you can only divide the fruits into groups of 1, giving each person 1 apple and 1 orange.
-
Scheduling: If event A repeats every 4 days and event B repeats every 9 days, the GCF helps determine when both events will occur on the same day. In this case, the events will coincide only after 36 days (the LCM).
-
Construction and Design: The GCF is used in various engineering and design tasks involving measurement and division of materials.
Conclusion
Finding the greatest common factor of 4 and 9, which is 1, might appear trivial at first glance. However, this seemingly simple calculation reveals the fundamental principles of number theory and its wide-ranging applications. Understanding the GCF and its relationship with other mathematical concepts, such as the LCM and relatively prime numbers, offers a deeper appreciation of the structure and relationships within the number system. Its importance extends far beyond basic arithmetic, impacting fields like algebra, computer science, and various real-world scenarios. Mastering the calculation of the GCF, through methods like listing factors, prime factorization, or the Euclidean algorithm, equips one with a valuable tool for solving more complex mathematical problems and understanding the fascinating world of numbers.
Latest Posts
Latest Posts
-
How Many Cups In 1 4 Lb Butter
May 14, 2025
-
Cuantos Block Es Un Metro Cuadrado
May 14, 2025
-
What Is 10 Of 24 Hours
May 14, 2025
-
How Many Hours Is 3000 Hours
May 14, 2025
-
What Is The Greatest Common Factor Of 28 And 36
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 4 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.