What Is The Greatest Common Factor Of 49 And 14
Treneri
May 10, 2025 · 6 min read
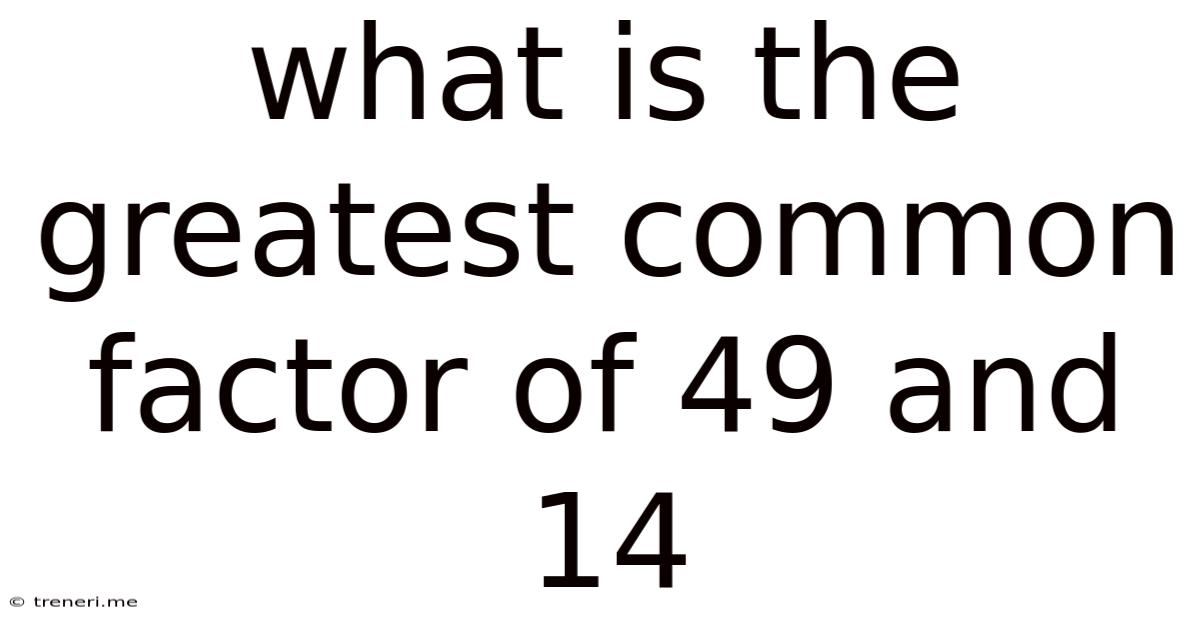
Table of Contents
What is the Greatest Common Factor (GCF) of 49 and 14? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory and has wide-ranging applications in mathematics and computer science. This article will thoroughly explore how to determine the GCF of 49 and 14, illustrating various methods and providing a broader understanding of the underlying principles. We'll move beyond simply finding the answer to delve into the theoretical underpinnings and practical uses of this mathematical operation.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Understanding the GCF is crucial for simplifying fractions, solving algebraic equations, and working with various mathematical concepts. It's a building block for more advanced mathematical ideas.
Methods for Finding the GCF of 49 and 14
Several methods can be employed to determine the GCF of 49 and 14. Let's explore the most common approaches:
1. Listing Factors Method
This is a straightforward method, especially useful for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 49: 1, 7, 49 Factors of 14: 1, 2, 7, 14
Comparing the lists, we see that the common factors are 1 and 7. The largest of these is 7. Therefore, the GCF of 49 and 14 is 7.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors (factors that are only divisible by 1 and themselves). The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 49: 7 x 7 = 7²
- Prime factorization of 14: 2 x 7
The only common prime factor is 7. The lowest power of 7 present in either factorization is 7¹ (or simply 7). Therefore, the GCF of 49 and 14 is 7.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 49 and 14:
- 49 ÷ 14 = 3 with a remainder of 7
- Now we replace the larger number (49) with the remainder (7). The new pair is 14 and 7.
- 14 ÷ 7 = 2 with a remainder of 0
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 7.
Why Understanding GCF is Important
The GCF has numerous practical applications across various fields:
-
Simplifying Fractions: The GCF allows us to simplify fractions to their lowest terms. For example, the fraction 14/49 can be simplified by dividing both the numerator and denominator by their GCF, which is 7, resulting in the simplified fraction 2/7.
-
Algebraic Simplification: GCF is crucial in simplifying algebraic expressions. It allows us to factor out common terms, making expressions easier to manipulate and solve.
-
Geometry and Measurement: GCF is used in geometry problems involving area, perimeter, and volume calculations. For example, determining the dimensions of the largest square tile that can perfectly cover a rectangular floor of given dimensions involves finding the GCF of the floor's length and width.
-
Cryptography and Computer Science: The GCF plays a significant role in cryptography, particularly in RSA encryption, which relies on the difficulty of factoring large numbers into their prime factors. Efficient GCF algorithms are essential for the security of these cryptographic systems.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, we simply find the prime factorization of each number and identify the common prime factors raised to the lowest power. For the Euclidean algorithm, we can iteratively apply it to pairs of numbers until we find the GCF of all numbers.
For example, to find the GCF of 49, 14, and 21:
- Prime factorization of 49: 7²
- Prime factorization of 14: 2 x 7
- Prime factorization of 21: 3 x 7
The only common prime factor is 7, and the lowest power is 7¹. Therefore, the GCF of 49, 14, and 21 is 7.
GCF and Least Common Multiple (LCM)
The GCF and the least common multiple (LCM) are closely related concepts. The LCM of two numbers is the smallest positive integer that is divisible by both numbers. There's a useful relationship between the GCF and LCM:
For any two integers 'a' and 'b', GCF(a, b) x LCM(a, b) = a x b
This relationship can be used to find the LCM of two numbers if their GCF is known, or vice versa. For 49 and 14:
GCF(49, 14) = 7 49 x 14 = 686 LCM(49, 14) = 686 / 7 = 98
Real-World Applications of GCF
Beyond the theoretical examples, let's consider some real-world scenarios where understanding GCF is essential:
-
Packaging: A manufacturer needs to package items into boxes of equal size. If they have 49 blue widgets and 14 red widgets, the largest number of widgets per box is the GCF(49, 14) = 7. They can create 7 boxes with 7 blue widgets and 2 red widgets in each.
-
Construction: A builder is laying out a rectangular garden. The length is 49 feet, and the width is 14 feet. The largest square tiles that will perfectly fit are of size GCF(49, 14) = 7 feet.
-
Music: In musical composition, the GCF helps determine the greatest common divisor of note values to simplify rhythmic notation.
Conclusion: Mastering the GCF
Finding the greatest common factor is a fundamental skill in mathematics with far-reaching applications. While finding the GCF of 49 and 14 might seem like a simple exercise, understanding the various methods—listing factors, prime factorization, and the Euclidean algorithm—provides a solid foundation for tackling more complex problems in number theory, algebra, geometry, and even computer science. The ability to efficiently calculate the GCF is a valuable asset for anyone working with numbers and mathematical concepts. Remember to choose the method best suited to the numbers involved for efficiency. The Euclidean algorithm shines for larger numbers, while the listing factors method is efficient for smaller ones. Mastering these concepts will undoubtedly enhance your mathematical problem-solving abilities.
Latest Posts
Latest Posts
-
550 Rounded To The Nearest Hundred
May 10, 2025
-
Volume Of Sphere With Radius 5
May 10, 2025
-
20 Percent Off Of 15 Dollars
May 10, 2025
-
What Percent Of 80 Is 6
May 10, 2025
-
Calculate The Heat Capacity Of The Calorimeter
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 49 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.