What Is The Greatest Common Factor Of 64 And 72
Treneri
May 10, 2025 · 5 min read
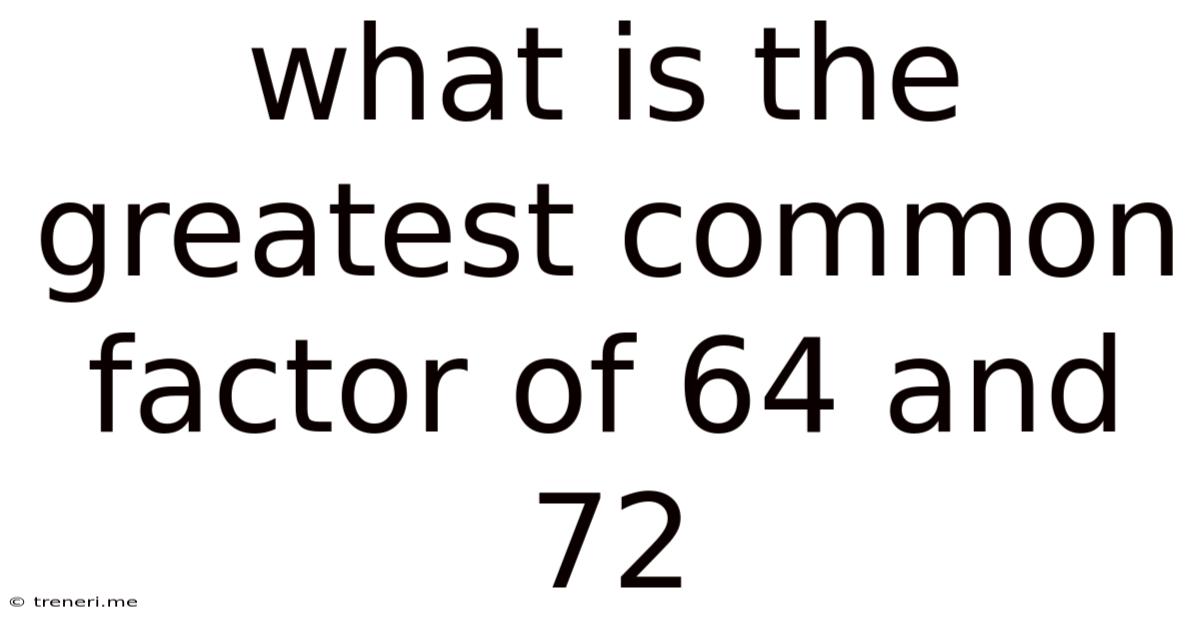
Table of Contents
What is the Greatest Common Factor of 64 and 72? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the underlying principles and various methods for solving it can be incredibly beneficial, especially in algebra, number theory, and even computer science. This in-depth exploration will not only answer the question – what is the greatest common factor of 64 and 72? – but also equip you with the knowledge and strategies to tackle similar problems with ease and confidence. We’ll delve into several methods, examining their strengths and weaknesses, and exploring the practical applications of GCF in various fields.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding number relationships.
Why is Finding the GCF Important?
The ability to efficiently find the GCF is vital in several areas:
- Simplifying Fractions: Reducing fractions to their simplest form requires finding the GCF of the numerator and denominator. This makes fractions easier to work with and understand.
- Algebraic Expressions: Factoring algebraic expressions often involves finding the GCF of the terms involved. This simplifies the expression and allows for further manipulation and solving.
- Number Theory: GCF is a cornerstone of number theory, with applications in cryptography and other advanced mathematical fields.
- Computer Science: Algorithms for finding the GCF are used in various computer science applications, particularly in cryptography and optimization problems.
Methods for Finding the GCF of 64 and 72
Let's explore several methods to determine the GCF of 64 and 72:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
Factors of 64: 1, 2, 4, 8, 16, 32, 64 Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
By comparing the lists, we can see that the common factors are 1, 2, 4, and 8. The greatest of these is 8. Therefore, the GCF of 64 and 72 is 8.
This method works well for smaller numbers but becomes cumbersome and time-consuming for larger numbers with many factors.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime Factorization of 64: 2 x 2 x 2 x 2 x 2 x 2 = 2<sup>6</sup> Prime Factorization of 72: 2 x 2 x 2 x 3 x 3 = 2<sup>3</sup> x 3<sup>2</sup>
The common prime factor is 2. The lowest power of 2 present in both factorizations is 2<sup>3</sup> = 8. Therefore, the GCF of 64 and 72 is 8.
This method is more efficient than the listing factors method, especially for larger numbers, as it systematically identifies the common prime factors.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 64 and 72:
- 72 - 64 = 8
- Now we find the GCF of 64 and 8.
- 64 - 8 = 56
- 56 - 8 = 48
- 48 - 8 = 40
- 40 - 8 = 32
- 32 - 8 = 24
- 24 - 8 = 16
- 16 - 8 = 8
- Now we have 8 and 8. Therefore, the GCF is 8.
While this specific implementation might seem lengthy, the Euclidean algorithm can be significantly more efficient for much larger numbers where listing factors or prime factorization would be impractical. Optimized versions of the Euclidean algorithm are frequently used in computer programs.
Applications of GCF
Understanding and applying the concept of GCF extends far beyond simple arithmetic. Its applications are numerous and impactful across different fields:
1. Simplifying Fractions in Mathematics
GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 64/72 can be simplified by dividing both the numerator and denominator by their GCF, which is 8. This simplifies the fraction to 8/9. This simplification is essential for easier calculations and understanding of the fraction's magnitude.
2. Factoring Algebraic Expressions in Algebra
Finding the GCF is an integral step in factoring algebraic expressions. For example, consider the expression 64x + 72y. The GCF of 64 and 72 is 8. Therefore, the expression can be factored as 8(8x + 9y). Factoring simplifies expressions and allows for further manipulation and solution finding in more complex algebraic equations.
3. Solving Diophantine Equations in Number Theory
Diophantine equations are algebraic equations where only integer solutions are sought. The GCF plays a significant role in determining the solvability and finding solutions to these equations. Understanding GCF helps in identifying conditions for the existence of integer solutions.
4. Cryptography and Computer Science
The Euclidean algorithm, used to efficiently calculate the GCF, is fundamental in many cryptographic algorithms. The RSA algorithm, a widely used public-key cryptography system, relies heavily on the efficiency of finding the GCF for secure encryption and decryption. The concept is also utilized in optimization problems within computer science.
Conclusion: Mastering the GCF
Finding the greatest common factor might seem like a rudimentary mathematical operation, but its importance extends far beyond basic arithmetic. Through understanding the different methods – listing factors, prime factorization, and the Euclidean algorithm – one can efficiently determine the GCF for various number pairs, irrespective of their size. This ability is crucial for simplifying fractions, factoring algebraic expressions, solving complex mathematical problems, and even contributing to advanced applications in computer science and cryptography. Mastering the concept of GCF is a fundamental step towards a deeper understanding of number theory and its numerous applications. The GCF of 64 and 72, as demonstrated through various methods, is definitively 8. Remember to select the most efficient method based on the numbers involved, prioritizing the Euclidean algorithm for larger numbers.
Latest Posts
Latest Posts
-
Como Saber Si Un Chihuahua Va A Ser Pequeno
May 10, 2025
-
Calculating Enthalpy Of Vaporization From Vapor Pressure
May 10, 2025
-
How Many Days Since May 21 2023
May 10, 2025
-
Cuantos Dias Faltan Para 6 De Agosto
May 10, 2025
-
Creatinine Conversion Mmol L To Mg Dl
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 64 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.