What Is The Greatest Common Factor Of 7 And 28
Treneri
May 10, 2025 · 4 min read
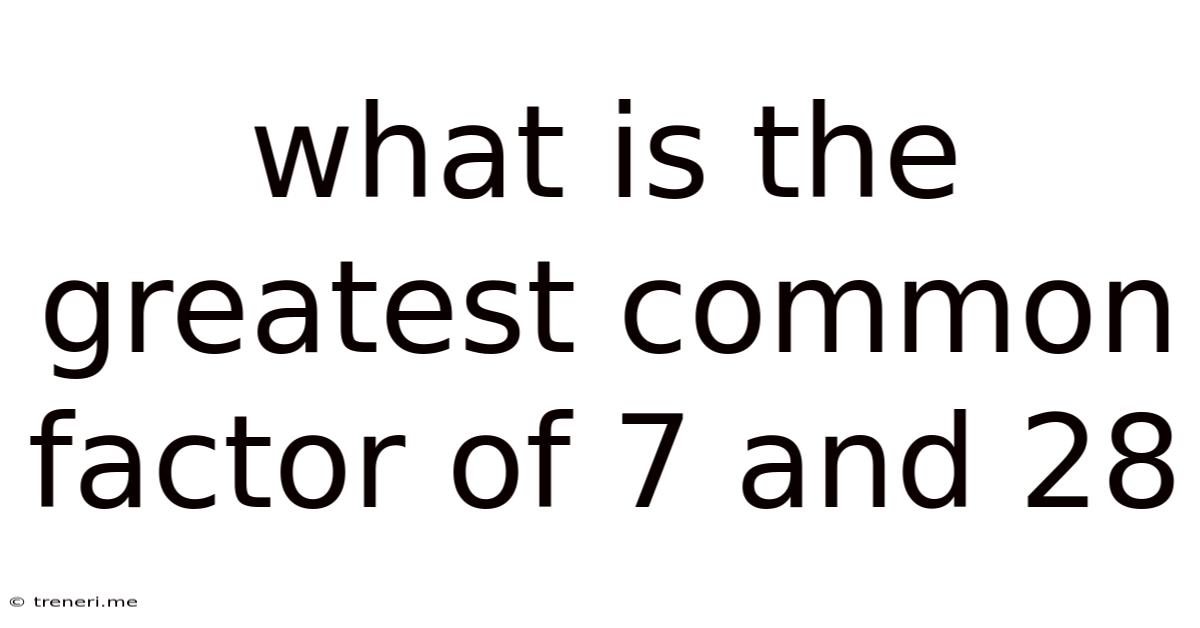
Table of Contents
What is the Greatest Common Factor of 7 and 28? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with far-reaching applications in mathematics and beyond. This article delves into the process of determining the GCF of 7 and 28, exploring various methods and illustrating the broader significance of this seemingly basic concept.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers perfectly. Understanding the GCF is crucial for simplifying fractions, solving algebraic equations, and working with various mathematical structures.
Methods for Finding the GCF
Several methods can be employed to find the GCF of two numbers. Let's explore some of the most common approaches, applying them to find the GCF of 7 and 28.
1. Listing Factors
The most straightforward method involves listing all the factors of each number and identifying the largest factor common to both.
- Factors of 7: 1, 7
- Factors of 28: 1, 2, 4, 7, 14, 28
Comparing the lists, we see that the common factors are 1 and 7. The greatest common factor is therefore 7.
2. Prime Factorization
This method involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves. The GCF is then found by multiplying the common prime factors raised to their lowest powers.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 28: 2 x 2 x 7 = 2² x 7
The only common prime factor is 7. Therefore, the GCF of 7 and 28 is 7.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is the GCF.
Let's apply the Euclidean algorithm to 7 and 28:
- 28 ÷ 7 = 4 with a remainder of 0
Since the remainder is 0, the GCF is the smaller number, which is 7.
The Euclidean algorithm is particularly efficient for larger numbers because it avoids the need to list all factors or find prime factorizations, which can be time-consuming for very large integers.
Significance of the GCF
The GCF has numerous applications across various mathematical fields and practical scenarios:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 28/7 can be simplified by dividing both the numerator and denominator by their GCF (7), resulting in the simplified fraction 4/1 or simply 4.
-
Solving Equations: The GCF plays a crucial role in solving algebraic equations, particularly those involving factoring polynomials. Finding the common factors allows us to simplify and solve these equations more effectively.
-
Modular Arithmetic: In modular arithmetic, the GCF is fundamental in determining whether a linear congruence has a solution.
-
Cryptography: The GCF and related concepts like the least common multiple (LCM) are crucial in modern cryptography algorithms, particularly in public-key cryptography systems like RSA.
-
Geometry: The GCF finds application in geometric problems involving finding the dimensions of the largest square that can tile a rectangle with given dimensions.
-
Real-World Applications: Beyond pure mathematics, the GCF has practical applications in various fields, including:
- Division of objects: Determining the maximum number of identical groups that can be formed from a set of objects.
- Resource allocation: Optimizing resource distribution based on common factors.
- Construction and design: Calculating the optimal dimensions for structures or designs.
Exploring Further: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. There's a useful relationship between the GCF and LCM of two numbers, a and b:
LCM(a, b) x GCF(a, b) = a x b
For 7 and 28:
- GCF(7, 28) = 7
- LCM(7, 28) = 28 (Since 28 is a multiple of both 7 and 28)
Let's verify the relationship:
7 x 28 = 196
7 x 28 = 196
The equation holds true. Understanding the relationship between GCF and LCM further enhances our grasp of number theory.
Conclusion: The Power of a Simple Concept
While finding the greatest common factor of 7 and 28 might appear trivial at first glance, the underlying concept carries significant weight in mathematics and beyond. This simple arithmetic operation forms the basis for more advanced mathematical concepts and finds applications in diverse fields. Mastering the methods for calculating the GCF, including listing factors, prime factorization, and the Euclidean algorithm, provides a strong foundation for further exploration of number theory and its practical applications. The seemingly simple act of determining that the GCF of 7 and 28 is 7 opens doors to a deeper understanding of the intricate world of numbers and their relationships. From simplifying fractions to securing digital communications, the GCF's influence is pervasive and profound.
Latest Posts
Latest Posts
-
Creatinine From Mmol L To Mg Dl
May 11, 2025
-
How Many Days From August 1 To December 31 2024
May 11, 2025
-
35 Kilometers Is How Many Miles
May 11, 2025
-
How Many Cbm In 40ft Container
May 11, 2025
-
How Do You Find The Exact Area Of A Circle
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 7 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.