What Is The Greatest Common Factor Of 8 14
Treneri
May 11, 2025 · 5 min read
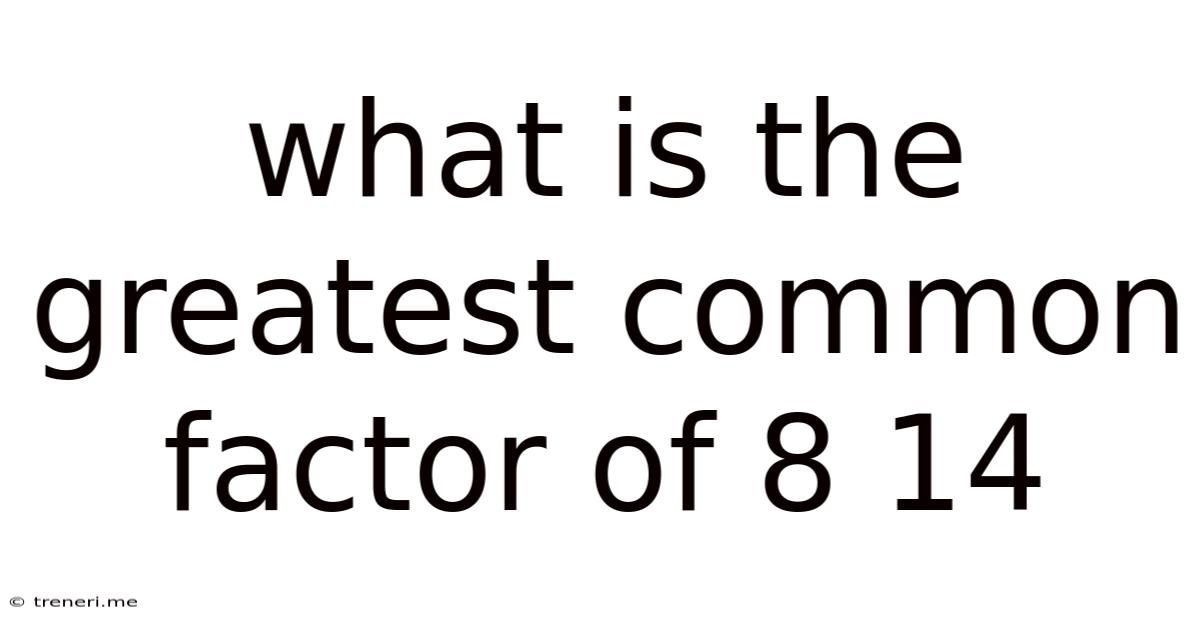
Table of Contents
What is the Greatest Common Factor of 8 and 14? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles unlocks a world of mathematical possibilities. This article delves deep into determining the GCF of 8 and 14, exploring various methods, and showcasing the broader significance of this concept in number theory and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding the relationships between numbers.
Methods for Finding the GCF of 8 and 14
Several methods exist for calculating the GCF, each offering a unique approach and level of complexity. Let's explore the most common ones in the context of finding the GCF of 8 and 14:
1. Listing Factors Method
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 8: 1, 2, 4, 8 Factors of 14: 1, 2, 7, 14
Comparing the lists, we see that the common factors are 1 and 2. The greatest common factor is therefore 2.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 14: 2 x 7
The only common prime factor is 2. Since the lowest power of 2 in either factorization is 2¹ (or simply 2), the GCF of 8 and 14 is 2.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of larger numbers. It relies on repeated division until the remainder is 0. The last non-zero remainder is the GCF.
- Divide the larger number (14) by the smaller number (8): 14 ÷ 8 = 1 with a remainder of 6.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (6): 8 ÷ 6 = 1 with a remainder of 2.
- Repeat the process: 6 ÷ 2 = 3 with a remainder of 0.
Since the last non-zero remainder is 2, the GCF of 8 and 14 is 2.
The Significance of the GCF
The seemingly simple task of finding the GCF has far-reaching implications across various mathematical fields:
1. Simplifying Fractions
The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 8/14 can be simplified by dividing both the numerator and the denominator by their GCF (2), resulting in the equivalent fraction 4/7.
2. Solving Diophantine Equations
Diophantine equations are algebraic equations where only integer solutions are sought. The GCF plays a vital role in determining the solvability and finding solutions to these equations.
3. Modular Arithmetic
Modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus), heavily relies on the GCF for various operations and theorems.
4. Cryptography
The GCF, specifically the Euclidean algorithm for finding it, is fundamental to many cryptographic algorithms. These algorithms are used to secure digital communication and data storage.
5. Abstract Algebra
In abstract algebra, the concept of the GCF extends to more complex algebraic structures, playing a crucial role in ring theory and ideal theory.
Beyond the Basics: Exploring Related Concepts
Understanding the GCF opens doors to other important concepts in number theory:
1. Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is a multiple of each of the integers. The GCF and LCM are related by the following formula:
LCM(a, b) = (a x b) / GCF(a, b)
For 8 and 14, the LCM is (8 x 14) / 2 = 56.
2. Relatively Prime Numbers (Coprime Numbers)
Two numbers are relatively prime (or coprime) if their GCF is 1. For example, 8 and 15 are relatively prime because their GCF is 1.
Practical Applications of GCF
The GCF isn't just a theoretical concept; it has numerous practical applications:
-
Dividing objects evenly: Imagine you have 8 apples and 14 oranges, and you want to divide them into equal groups without any leftovers. The GCF (2) tells you that you can create a maximum of 2 equal groups.
-
Simplifying recipes: If a recipe calls for 8 cups of flour and 14 cups of sugar, but you want to reduce the recipe's size, the GCF helps determine the largest reduction factor that keeps the ingredient ratios unchanged.
-
Scheduling: The GCF can be useful in scheduling tasks or events that need to occur at regular intervals.
Conclusion: The Power of Simplicity
While finding the greatest common factor of 8 and 14 might seem like a minor mathematical exercise, it reveals the profound power of fundamental concepts in number theory. Understanding the various methods for calculating the GCF, its significance in simplifying fractions, solving equations, and its application in more advanced mathematical fields, underscores its importance in various disciplines, from cryptography to abstract algebra. Its seemingly simple nature masks a depth and breadth of application that make it a cornerstone of mathematical understanding. The GCF, therefore, is far more than just a simple calculation; it’s a key that unlocks a world of mathematical possibilities.
Latest Posts
Latest Posts
-
How To Find Area Of A Triangle In Coordinate Geometry
May 11, 2025
-
How Long Is A Thousand Hours
May 11, 2025
-
Find The Surface Area To The Nearest Whole Number
May 11, 2025
-
Least Common Multiple Of 4 8 And 10
May 11, 2025
-
What Does 1 Cup Of Popcorn Look Like
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 8 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.