What Is The Greatest Common Factor Of 8 And 52
Treneri
May 09, 2025 · 5 min read
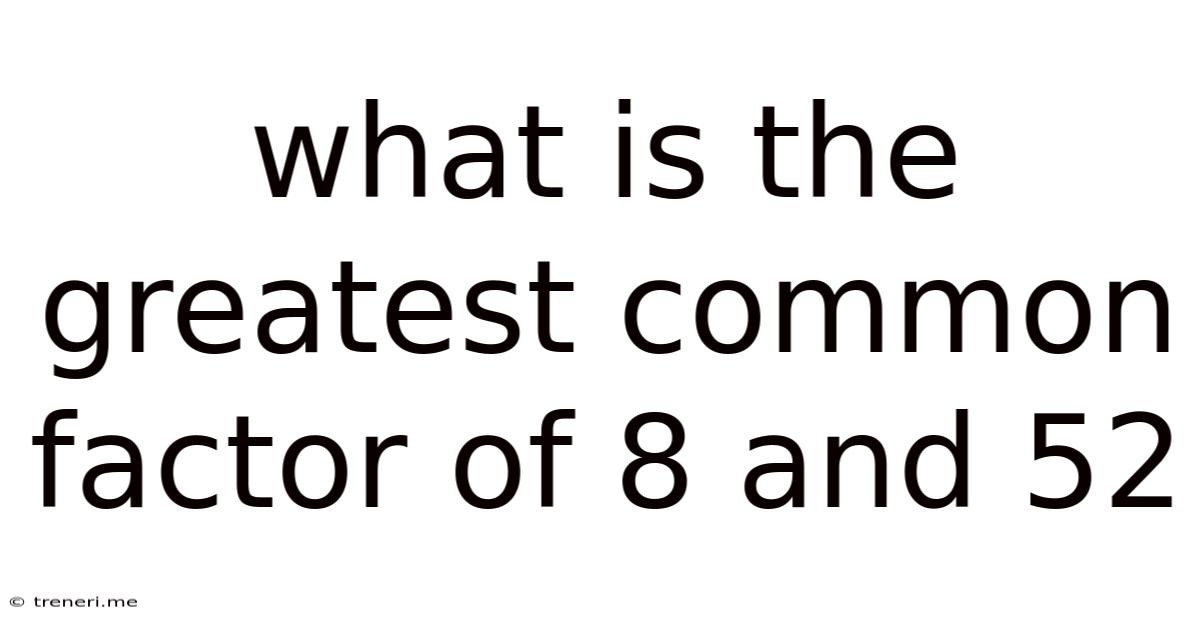
Table of Contents
What is the Greatest Common Factor of 8 and 52? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and exploring different methods for calculating the GCF reveals a fascinating glimpse into number theory, a branch of mathematics with far-reaching implications. This article will delve into the concept of GCF, focusing specifically on finding the GCF of 8 and 52, and then expanding on various techniques applicable to a broader range of numbers.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers perfectly. For instance, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The greatest among these is 6, making 6 the GCF of 12 and 18.
This concept is fundamental in various mathematical applications, including simplifying fractions, solving algebraic equations, and understanding modular arithmetic. Understanding GCF is also crucial in areas outside pure mathematics, such as computer science (especially in algorithms and data structures) and cryptography.
Finding the GCF of 8 and 52: A Step-by-Step Approach
Let's focus on the specific problem: finding the GCF of 8 and 52. We can use several methods to achieve this.
1. Listing Factors Method
This is a straightforward approach, especially for smaller numbers. We list all the factors of each number and identify the largest factor common to both.
Factors of 8: 1, 2, 4, 8 Factors of 52: 1, 2, 4, 13, 26, 52
By comparing the lists, we can see that the common factors are 1, 2, and 4. The largest among these is 4. Therefore, the GCF of 8 and 52 is 4.
This method is effective for small numbers, but it becomes cumbersome and inefficient when dealing with larger numbers.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors. The prime factors are the building blocks of a number, and they are prime numbers (numbers divisible only by 1 and themselves). Once we have the prime factorization of each number, we identify the common prime factors and multiply them together to get the GCF.
Prime factorization of 8: 2 x 2 x 2 = 2³ Prime factorization of 52: 2 x 2 x 13 = 2² x 13
The common prime factor is 2, appearing twice in the factorization of 8 (2³) and twice in the factorization of 52 (2²). We take the minimum power of the common prime factor which is 2².
Therefore, the GCF of 8 and 52 is 2² = 4.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where the listing factors or prime factorization methods become less practical. The algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 8 and 52:
- Divide the larger number (52) by the smaller number (8): 52 ÷ 8 = 6 with a remainder of 4.
- Replace the larger number with the remainder: Now we find the GCF of 8 and 4.
- Repeat the process: 8 ÷ 4 = 2 with a remainder of 0.
- The GCF is the last non-zero remainder: Since the remainder is 0, the GCF is the previous remainder, which is 4.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers. Its efficiency stems from reducing the size of the numbers involved in each step.
Expanding the Concept: GCF Applications and Further Exploration
The concept of GCF extends beyond simple arithmetic problems. It has significant applications in various mathematical areas and related fields.
1. Simplifying Fractions
The GCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, to simplify the fraction 52/8, we find the GCF of 52 and 8 (which is 4), and then divide both the numerator and the denominator by 4: 52/4 = 13 and 8/4 = 2. Therefore, 52/8 simplifies to 13/2.
2. Solving Linear Diophantine Equations
Linear Diophantine equations are equations of the form ax + by = c, where a, b, and c are integers, and we are looking for integer solutions for x and y. The GCF of a and b plays a crucial role in determining the existence and nature of the solutions. If c is not divisible by the GCF of a and b, then there are no integer solutions. If c is divisible by the GCF of a and b, there are infinitely many integer solutions.
3. Modular Arithmetic and Cryptography
The concept of GCF is fundamental in modular arithmetic, which involves arithmetic operations with remainders. This has direct applications in cryptography, particularly in the RSA algorithm, a widely used public-key cryptosystem. The security of RSA relies heavily on the difficulty of factoring large numbers into their prime factors – a problem closely related to finding the GCF.
4. Computer Science Algorithms
The Euclidean algorithm, used to find the GCF, is a classic example of an efficient algorithm in computer science. Its simplicity and efficiency make it valuable in various applications, including data structures and numerical computations.
Conclusion: The Power of a Simple Concept
While finding the greatest common factor of 8 and 52 might seem like a rudimentary task, the underlying principles and broader applications reveal its significance in various fields. The different methods – listing factors, prime factorization, and the Euclidean algorithm – each offer valuable insights into number theory and the efficiency of different computational approaches. Understanding the GCF is not just about solving a single problem; it's about grasping a foundational concept that unlocks a deeper understanding of numbers and their relationships, leading to a more profound appreciation of mathematics and its far-reaching influence. From simplifying fractions to securing online transactions, the GCF plays a vital, often unseen, role in many aspects of our modern world.
Latest Posts
Latest Posts
-
How Long Ago Was 1979 In Years
May 11, 2025
-
Quantos Dias Faltam Para O Natal De 2024
May 11, 2025
-
Cuanto Falta Para 31 De Diciembre
May 11, 2025
-
8 2 3 As A Fraction
May 11, 2025
-
Cuanto Son 5 5 Pies En Centimetros
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 8 And 52 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.