What Is The Greatest Common Factor Of 84 And 90
Treneri
May 13, 2025 · 5 min read
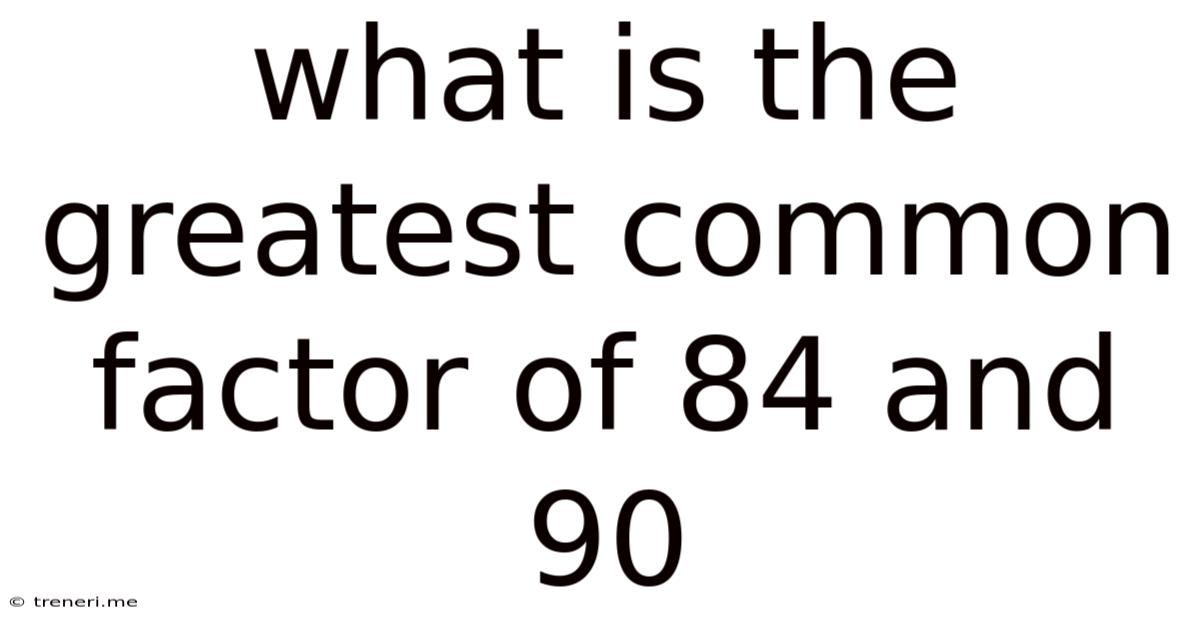
Table of Contents
What is the Greatest Common Factor (GCF) of 84 and 90? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications spanning various fields, from cryptography to computer science. This article will delve into the process of determining the GCF of 84 and 90, exploring multiple methods and expanding on the broader mathematical principles involved. We’ll go beyond simply providing the answer, focusing on understanding why the answer is what it is.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Why is finding the GCF important?
The GCF has numerous applications across diverse fields:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. Dividing both the numerator and the denominator by their GCF reduces the fraction to its simplest form.
-
Algebraic Simplification: In algebra, the GCF is used to factor expressions, simplifying them and making them easier to manipulate.
-
Solving Diophantine Equations: These are equations where only integer solutions are sought. The GCF plays a significant role in determining the solvability and finding the solutions of these equations.
-
Cryptography: The concept of GCF underlies some cryptographic algorithms, particularly those based on modular arithmetic.
-
Computer Science: Algorithms for finding the GCF are used in various computer science applications, including tasks related to data structures and algorithms.
Methods for Finding the GCF of 84 and 90
Several methods can be employed to find the GCF of 84 and 90. Let's explore the most common ones:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
By comparing the two lists, we can see that the common factors are 1, 2, 3, and 6. The greatest common factor is therefore 6.
This method is straightforward for smaller numbers, but it becomes cumbersome and time-consuming as the numbers get larger.
2. Prime Factorization Method
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
Prime factorization of 84:
84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7 = 2² x 3 x 7
Prime factorization of 90:
90 = 2 x 45 = 2 x 3 x 15 = 2 x 3 x 3 x 5 = 2 x 3² x 5
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹. Therefore, the GCF is 2 x 3 = 6.
This method is more efficient than the listing factors method, especially for larger numbers. It provides a systematic approach to finding the GCF.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 84 and 90:
- 90 = 84 x 1 + 6 (Subtract 84 from 90, leaving a remainder of 6)
- 84 = 6 x 14 + 0 (Divide 84 by 6, leaving a remainder of 0)
The last non-zero remainder is 6, which is the GCF of 84 and 90.
The Euclidean algorithm is particularly efficient for large numbers because it reduces the size of the numbers at each step, leading to a quicker solution. It's the preferred method for computational purposes.
Expanding on the Concept: Beyond the GCF of 84 and 90
The GCF is a stepping stone to understanding more complex number theory concepts. Let's explore some related ideas:
Least Common Multiple (LCM)
The least common multiple (LCM) of two integers is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are related through the following formula:
GCF(a, b) x LCM(a, b) = a x b
Using this formula, we can find the LCM of 84 and 90:
6 x LCM(84, 90) = 84 x 90 LCM(84, 90) = (84 x 90) / 6 = 1260
Therefore, the LCM of 84 and 90 is 1260.
Relatively Prime Numbers
Two numbers are considered relatively prime (or coprime) if their greatest common factor is 1. For example, 15 and 28 are relatively prime because their GCF is 1. Understanding relative primality is essential in various mathematical applications.
Applications in Cryptography and Security
The GCF, particularly the Euclidean algorithm for its efficient computation, plays a crucial role in public-key cryptography. Algorithms like the RSA encryption system rely on the difficulty of finding the prime factors of a very large number (the product of two large prime numbers). The GCF helps in verifying the primality of these numbers, a crucial part of the security of these systems.
Conclusion: Mastering the GCF
Finding the greatest common factor of two numbers is a fundamental skill with far-reaching applications. We've explored three different methods – listing factors, prime factorization, and the Euclidean algorithm – each providing a unique approach to solving this problem. Understanding these methods not only allows you to find the GCF of 84 and 90 (which is 6) but also equips you with the knowledge to tackle more complex number theory problems and appreciate its relevance in various fields. The GCF is not just an isolated concept; it's a key building block in understanding broader mathematical principles and their applications in the real world. Remember to choose the method most suitable for the numbers involved, with the Euclidean algorithm being the most efficient for larger numbers. The understanding gained from this exploration extends far beyond the simple calculation itself.
Latest Posts
Latest Posts
-
Find The Difference Between 303 And 184
May 13, 2025
-
How To Find The Length Indicated
May 13, 2025
-
What Is The Factor Of 71
May 13, 2025
-
31 Km To Miles Per Hour
May 13, 2025
-
What Size Rug For 10x12 Room
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 84 And 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.