What Is The Greatest Common Factor Of 9 And 4
Treneri
May 13, 2025 · 5 min read
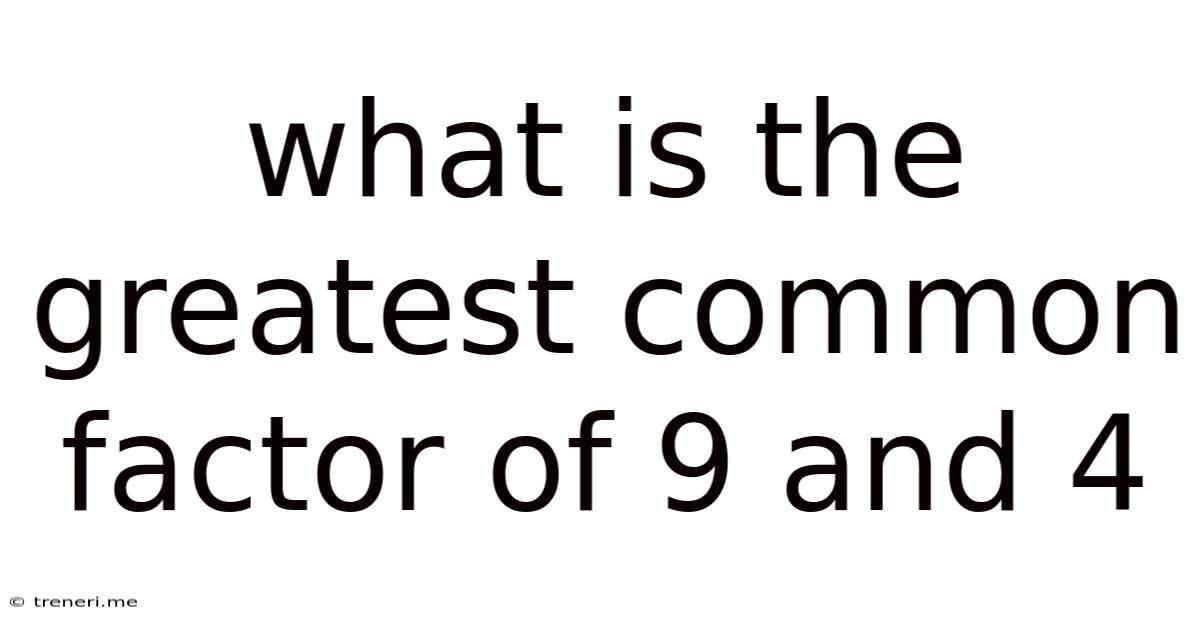
Table of Contents
What is the Greatest Common Factor of 9 and 4? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple task, especially when dealing with smaller numbers like 9 and 4. However, understanding the underlying concepts and different methods for calculating the GCF provides a valuable foundation in number theory and has practical applications in various fields, from simplifying fractions to solving complex mathematical problems. This article will explore the GCF of 9 and 4 in detail, examining multiple approaches and highlighting the broader significance of this fundamental concept.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. This concept is crucial in simplifying fractions, factoring polynomials, and solving various mathematical problems.
Why is the GCF Important?
The GCF plays a critical role in simplifying fractions. For instance, if you have the fraction 12/18, finding the GCF (which is 6) allows you to simplify the fraction to its lowest terms (2/3). This simplification makes working with fractions easier and more efficient.
Beyond fractions, the GCF is essential in abstract algebra and number theory, forming the basis for many advanced concepts and algorithms. Understanding the GCF improves your overall mathematical understanding and problem-solving skills.
Calculating the GCF of 9 and 4: Methods and Explanation
Several methods can be used to find the GCF of 9 and 4. Let's explore the most common ones:
1. Listing Factors
This method involves listing all the factors of each number and identifying the largest factor they have in common.
Factors of 9: 1, 3, 9 Factors of 4: 1, 2, 4
Comparing the lists, we see that the only common factor is 1. Therefore, the GCF of 9 and 4 is 1.
2. Prime Factorization
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 4: 2 x 2 = 2²
Since 9 and 4 share no common prime factors, their GCF is 1.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 9 and 4:
- Divide 9 by 4: 9 = 4 x 2 + 1
- Divide 4 by the remainder 1: 4 = 1 x 4 + 0
The last non-zero remainder is 1, so the GCF of 9 and 4 is 1.
Relatively Prime Numbers
Two numbers are considered relatively prime or coprime if their greatest common factor is 1. Since the GCF of 9 and 4 is 1, they are relatively prime. This means they share no common factors other than 1.
Practical Applications of GCF
The concept of GCF extends far beyond simple number theory. Here are some real-world applications:
1. Simplifying Fractions
As mentioned earlier, the GCF is essential for simplifying fractions to their lowest terms. This makes calculations easier and improves understanding.
2. Geometry and Measurement
GCF finds application in solving geometry problems. For example, when determining the dimensions of the largest square tile that can perfectly cover a rectangular floor with specific dimensions, the GCF of the dimensions is used.
3. Cryptography
The concept of relatively prime numbers plays a crucial role in certain cryptographic algorithms. The security of these algorithms relies on the difficulty of finding the GCF of very large numbers.
4. Scheduling Problems
GCF can help solve scheduling problems where events need to occur at regular intervals. Finding the GCF can help determine the earliest time when both events will occur simultaneously.
5. Computer Science
The Euclidean algorithm, used for GCF calculation, is an efficient and fundamental algorithm used in various computer science applications, including cryptography and computer graphics.
Beyond the Basics: Exploring Further Concepts
Understanding the GCF opens doors to more advanced mathematical concepts:
1. Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is a multiple of each of the given integers. The GCF and LCM are related by the formula: LCM(a, b) = (a x b) / GCF(a, b). In the case of 9 and 4, the LCM is (9 x 4) / 1 = 36.
2. Modular Arithmetic
Modular arithmetic, which involves operations on remainders after division, relies heavily on the concept of GCF. The GCF plays a key role in determining the properties of modular arithmetic systems.
3. Diophantine Equations
Diophantine equations are equations where solutions are restricted to integers. The GCF is often used in determining the solvability of certain Diophantine equations.
Conclusion: The Significance of a Seemingly Simple Concept
While finding the GCF of 9 and 4 might appear trivial, the underlying concept and the methods used to calculate it are fundamental to number theory and have far-reaching applications in mathematics and other fields. Understanding the GCF provides a strong foundation for tackling more complex mathematical problems and expands your appreciation for the intricate connections within the world of numbers. The fact that 9 and 4 are relatively prime – a consequence of their GCF being 1 – highlights a key characteristic that influences their behavior in various mathematical contexts. From simplifying fractions to advanced cryptographic techniques, the GCF’s significance transcends its seemingly simple definition, making it a cornerstone of mathematical understanding. The exploration of the GCF, even in a seemingly simple case like 9 and 4, offers a valuable opportunity to delve deeper into the fascinating world of number theory.
Latest Posts
Latest Posts
-
Alos Cuantos Meses Pare Una Perra
May 13, 2025
-
120 Days From May 30 2024
May 13, 2025
-
How Many Square Feet Is 4x8
May 13, 2025
-
How Many Days In 3000 Hours
May 13, 2025
-
10k A Year Is How Much An Hour
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 9 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.