What Is The Lcm Of 2 And 11
Treneri
May 10, 2025 · 5 min read
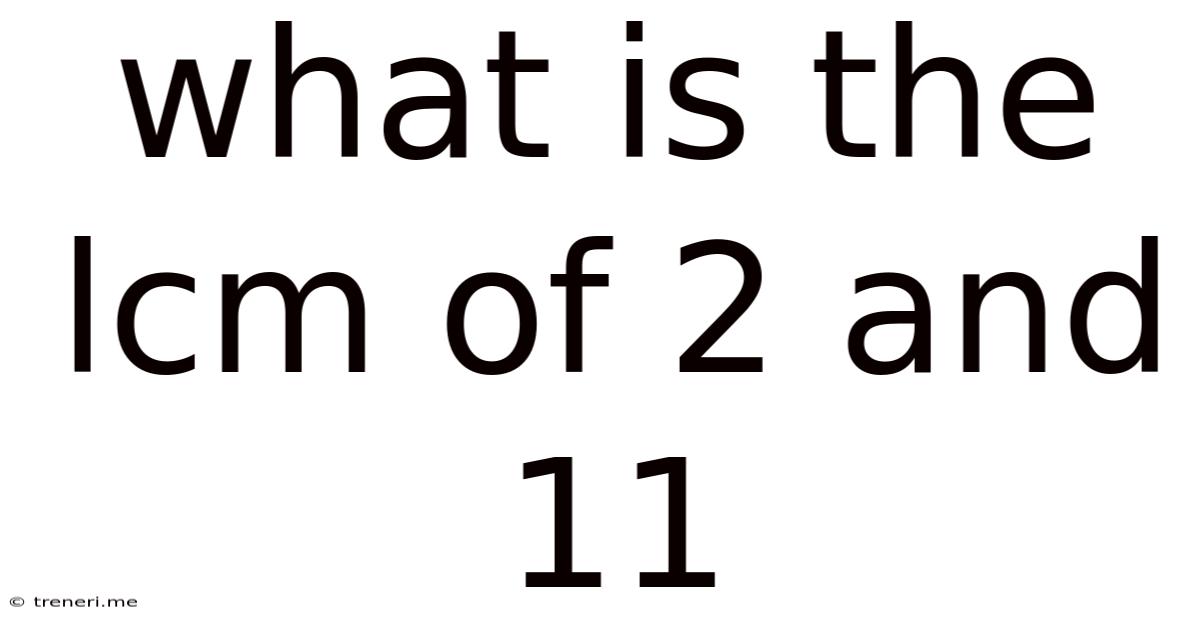
Table of Contents
What is the LCM of 2 and 11? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods for calculation can unlock a deeper appreciation of number theory and its applications. This article delves into the question: What is the LCM of 2 and 11? We'll not only answer this specific question but also explore various approaches to finding the LCM, examining their advantages and disadvantages, and broadening our understanding of this fundamental mathematical concept.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 2 and 11, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors.
For example, let's consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, 24... and the multiples of 6 are 6, 12, 18, 24, 30... Notice that 12 and 24 are common multiples of both 4 and 6. However, 12 is the smallest, making it the least common multiple (LCM) of 4 and 6.
Finding the LCM of 2 and 11: Methods and Approaches
Now, let's focus on the specific question: What is the LCM of 2 and 11? We can employ several methods to determine this.
Method 1: Listing Multiples
The most straightforward approach is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 22, 24, 26...
- Multiples of 11: 11, 22, 33, 44, 55...
As we can see, the smallest number that appears in both lists is 22. Therefore, the LCM of 2 and 11 is 22.
This method is simple and intuitive, especially for smaller numbers. However, it becomes less efficient as the numbers get larger. Imagine trying to find the LCM of 147 and 252 using this method – it would be quite tedious!
Method 2: Prime Factorization
A more sophisticated and efficient method involves prime factorization. This method is particularly useful for larger numbers.
- Prime factorization of 2: 2 (2 is a prime number)
- Prime factorization of 11: 11 (11 is a prime number)
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the numbers. In this case, we have:
- 2¹
- 11¹
The LCM is the product of these highest powers: 2¹ * 11¹ = 22
This method is more efficient than listing multiples, especially when dealing with larger numbers. It also provides a deeper understanding of the relationship between the numbers and their prime factors.
Method 3: Using the Formula (LCM and GCD Relationship)
The least common multiple (LCM) and the greatest common divisor (GCD) of two numbers are closely related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This can be expressed as:
LCM(a, b) * GCD(a, b) = a * b
where 'a' and 'b' are the two numbers.
First, we need to find the GCD of 2 and 11. Since 2 and 11 are both prime numbers and have no common factors other than 1, their GCD is 1.
Now, we can use the formula:
LCM(2, 11) * GCD(2, 11) = 2 * 11
LCM(2, 11) * 1 = 22
Therefore, LCM(2, 11) = 22
This method leverages the relationship between LCM and GCD, offering another efficient way to calculate the LCM. It's particularly helpful when dealing with numbers where finding the GCD is relatively easy.
Applications of LCM
Understanding and calculating LCMs isn't just an academic exercise; it has practical applications in various fields:
-
Scheduling: Imagine you have two machines that operate on cycles. Machine A completes a cycle every 2 hours, and Machine B completes a cycle every 11 hours. To determine when both machines will complete a cycle simultaneously, you need to find the LCM of 2 and 11, which is 22 hours.
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. This simplifies the addition or subtraction process.
-
Modular Arithmetic: LCMs play a crucial role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Music Theory: LCM is used in music theory to determine the least common multiple of rhythmic patterns, aiding in understanding and creating complex musical structures.
Expanding the Concept: LCM of More Than Two Numbers
The concepts and methods discussed so far can be extended to find the LCM of more than two numbers. For example, let's find the LCM of 2, 3, and 6.
Method 1: Listing Multiples: This method becomes even more cumbersome with more numbers.
Method 2: Prime Factorization: This remains an efficient method. The prime factorizations are:
- 2 = 2¹
- 3 = 3¹
- 6 = 2¹ * 3¹
The highest powers of the prime factors are 2¹ and 3¹. Therefore, the LCM(2, 3, 6) = 2¹ * 3¹ = 6
Method 3: Stepwise Approach: You can find the LCM of two numbers at a time. For example, first find LCM(2,3)=6, then find the LCM(6,6)=6.
Conclusion: The Power of Understanding LCM
The seemingly simple question, "What is the LCM of 2 and 11?" opens up a world of mathematical concepts and practical applications. We've explored various methods for finding the LCM, highlighting their advantages and disadvantages. Understanding LCMs is fundamental to various areas, from scheduling and fraction arithmetic to more complex fields like cryptography and music theory. Mastering the calculation of LCMs not only strengthens your mathematical skills but also enhances your problem-solving abilities across diverse disciplines. The answer to our initial question remains consistent across all methods: the LCM of 2 and 11 is indeed 22. By understanding the underlying principles and applying the appropriate methods, you can confidently tackle even more complex LCM problems.
Latest Posts
Latest Posts
-
How Many Square Miles In A Square Kilometer
May 10, 2025
-
Como Hallar La Distancia Entre Dos Puntos
May 10, 2025
-
Convert Mg L To Mg Ml
May 10, 2025
-
6 7 Km Is How Many Miles
May 10, 2025
-
Good Uv Index To Get Tan
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 2 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.