What Is The Lcm Of 3 5 11
Treneri
May 13, 2025 · 5 min read
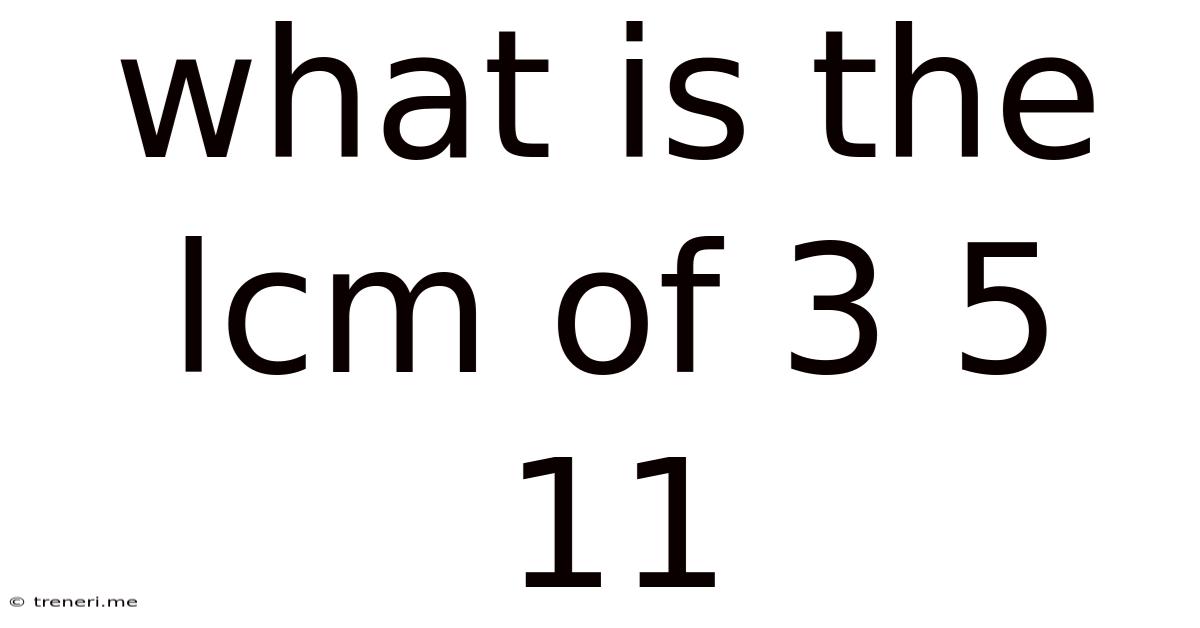
Table of Contents
What is the LCM of 3, 5, and 11? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications ranging from simple fraction addition to complex scheduling problems. This article will explore the LCM of 3, 5, and 11 in detail, explaining the various methods for calculating it and highlighting its significance in different mathematical contexts. We'll delve into the underlying principles, provide step-by-step examples, and explore related concepts to build a comprehensive understanding.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 3, 5, and 11, let's establish a solid understanding of what an LCM is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18... The smallest of these common multiples is 6, hence the LCM of 2 and 3 is 6.
Methods for Finding the LCM
Several methods exist for calculating the LCM, each with its own advantages depending on the numbers involved. Let's examine the most common approaches:
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers. You list the multiples of each number until you find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, ...
- Multiples of 11: 11, 22, 33, 44, 55, ...
By inspecting the lists, we can see that the smallest common multiple of 3, 5, and 11 is 165.
This method becomes less practical with larger numbers as the lists can get quite lengthy.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 11: 11 (11 is a prime number)
Since 3, 5, and 11 are all prime numbers and have no common factors, the LCM is simply the product of these numbers:
LCM(3, 5, 11) = 3 × 5 × 11 = 165
This method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers or a greater number of integers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be extended to more than two numbers, although the calculation becomes slightly more complex. Since 3, 5, and 11 are all prime numbers, their GCD is 1. Therefore, this method isn't particularly helpful in this specific case, but it's important to understand the relationship between LCM and GCD for more complex scenarios.
The LCM of 3, 5, and 11 in Different Contexts
The LCM has practical applications in various mathematical and real-world situations. Let's explore some examples:
1. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, you need to find a common denominator, which is usually the LCM of the denominators. For example, adding 1/3 + 1/5 + 1/11 requires finding the LCM of 3, 5, and 11 (which is 165). The fractions would then be rewritten as 55/165 + 33/165 + 15/165, allowing for easy addition.
2. Cyclic Events
Imagine three events that occur cyclically: Event A every 3 days, Event B every 5 days, and Event C every 11 days. The LCM (165) represents the number of days until all three events occur on the same day again.
3. Scheduling and Synchronization
In project management or scheduling tasks, the LCM can determine the shortest time interval required for synchronized completion of multiple tasks with different cycle times.
Expanding the Concept: LCM of More Than Three Numbers
The methods described above can be extended to find the LCM of more than three numbers. The prime factorization method remains particularly efficient. For example, to find the LCM of 3, 5, 11, and 7, you would find the prime factorization of each number and then multiply the highest power of each prime factor present in any of the factorizations.
Conclusion: The Power of the LCM
The least common multiple is a seemingly simple mathematical concept, yet it underpins many important calculations and problem-solving techniques across various fields. Understanding the different methods for calculating the LCM, particularly the prime factorization method, is crucial for efficiently solving problems involving multiples, fractions, cyclic events, and synchronization tasks. The ability to find the LCM of 3, 5, and 11 (and other sets of numbers) demonstrates a fundamental understanding of number theory and its practical applications. This knowledge provides a solid foundation for tackling more advanced mathematical concepts and real-world challenges. The simple calculation of finding the LCM of 3, 5, and 11, resulting in 165, serves as a gateway to appreciating the power and utility of this essential mathematical tool. Remember to practice these methods with different sets of numbers to solidify your understanding and improve your problem-solving skills.
Latest Posts
Latest Posts
-
Circles Circumference Divided By Its Diameter
May 13, 2025
-
6 Out Of 20 As A Grade
May 13, 2025
-
Cuanto Es 8 Oz En Ml
May 13, 2025
-
What Is A 10 Out Of 14 As A Grade
May 13, 2025
-
How Many Months Are In 35 Years
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 5 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.