What Is The Lcm Of 5 And 11
Treneri
May 13, 2025 · 5 min read
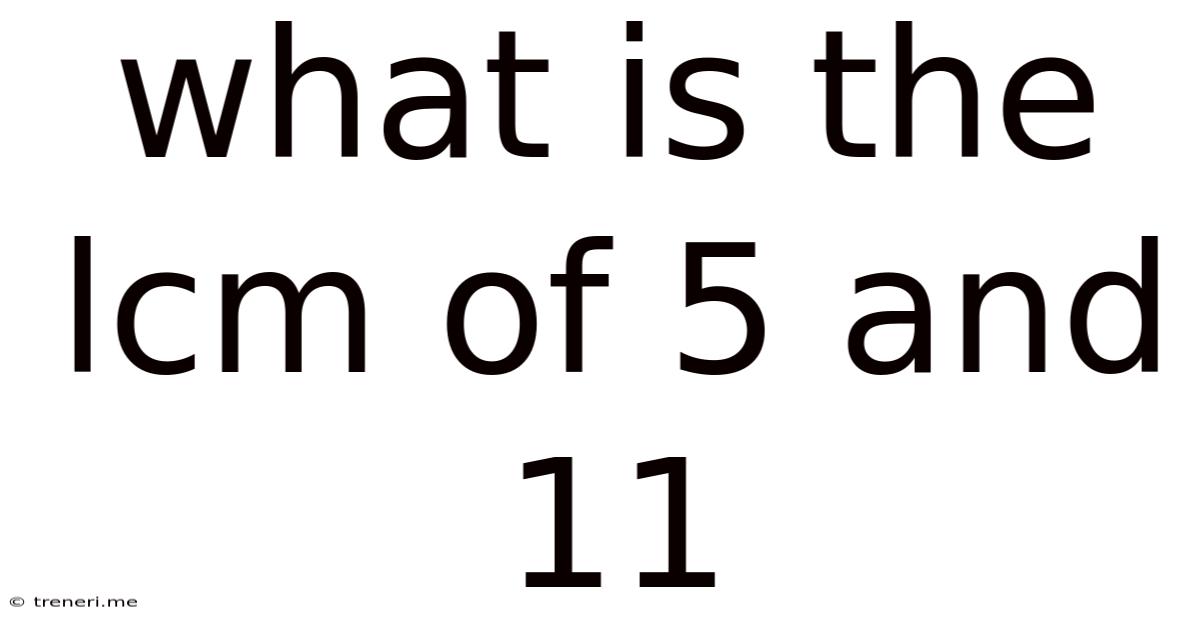
Table of Contents
What is the LCM of 5 and 11? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it offers valuable insights into number theory and its applications. This article will explore the LCM of 5 and 11, delving into various approaches, and expanding on the broader significance of LCMs in mathematics and beyond.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. It's a fundamental concept in mathematics with applications ranging from simplifying fractions to solving problems in areas like scheduling and music theory.
Consider two numbers, 'a' and 'b'. Their LCM is denoted as LCM(a, b). For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Calculating the LCM of 5 and 11
The numbers 5 and 11 are both prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This characteristic significantly simplifies the process of finding their LCM.
Method 1: Listing Multiples
The simplest method to find the LCM is by listing the multiples of each number until a common multiple is found.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60...
- Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110...
Observing the lists, we see that the smallest common multiple of 5 and 11 is 55. Therefore, LCM(5, 11) = 55.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM of larger numbers. It involves expressing each number as a product of its prime factors. Since 5 and 11 are already prime numbers, their prime factorizations are simply:
- 5 = 5¹
- 11 = 11¹
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the numbers. In this case, we have 5¹ and 11¹. Multiplying these highest powers together gives us the LCM:
LCM(5, 11) = 5¹ * 11¹ = 55
Method 3: Using the Formula with Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are related by the following formula:
LCM(a, b) * GCD(a, b) = a * b
The greatest common divisor (GCD) is the largest positive integer that divides both 'a' and 'b' without leaving a remainder. Since 5 and 11 are prime numbers and have no common factors other than 1, their GCD is 1.
Therefore:
LCM(5, 11) * GCD(5, 11) = 5 * 11 LCM(5, 11) * 1 = 55 LCM(5, 11) = 55
The Significance of LCM
The concept of LCM extends far beyond simple arithmetic exercises. Its applications are widespread and crucial in various fields:
1. Fraction Simplification and Addition/Subtraction
Finding the LCM is essential when adding or subtracting fractions with different denominators. The LCM of the denominators becomes the common denominator, allowing for easy addition or subtraction.
For example, to add 1/5 and 1/11, we find the LCM of 5 and 11 (which is 55). Then we rewrite the fractions with the common denominator:
(1/5) + (1/11) = (11/55) + (5/55) = 16/55
2. Scheduling and Cyclical Events
LCM plays a vital role in solving scheduling problems involving recurring events. For instance, if two events occur at intervals of 5 days and 11 days respectively, the LCM (55 days) represents the time it takes for both events to occur on the same day again.
3. Music Theory
In music, the LCM helps in determining the least common period of two or more musical rhythms or phrases. This is crucial for creating harmonious and rhythmic compositions.
Expanding on Prime Numbers and their Role in LCM Calculations
The fact that 5 and 11 are prime numbers simplifies the LCM calculation considerably. If the numbers were composite (non-prime), the process would involve more steps in prime factorization. Let's examine a scenario with composite numbers to illustrate this:
Let's find the LCM of 12 and 18.
Method 1: Prime Factorization:
- 12 = 2² * 3¹
- 18 = 2¹ * 3²
The highest power of 2 is 2², and the highest power of 3 is 3². Therefore:
LCM(12, 18) = 2² * 3² = 4 * 9 = 36
Method 2: Listing Multiples:
- Multiples of 12: 12, 24, 36, 48, 60...
- Multiples of 18: 18, 36, 54, 72...
The least common multiple is 36.
Beyond Two Numbers: Extending LCM to Multiple Numbers
The concept of LCM can be extended to more than two numbers. For example, to find the LCM of 5, 11, and 15:
-
Prime Factorization:
- 5 = 5¹
- 11 = 11¹
- 15 = 3¹ * 5¹
-
Identify Highest Powers: The highest powers are 3¹, 5¹, and 11¹.
-
Calculate LCM: LCM(5, 11, 15) = 3¹ * 5¹ * 11¹ = 165
Conclusion: The Ubiquity of LCM
The seemingly straightforward calculation of the LCM of 5 and 11 opens a window into a rich area of mathematics. From its fundamental role in arithmetic operations to its applications in various fields, the least common multiple proves its importance as a concept with widespread practical significance. Understanding the different methods for calculating the LCM equips us with valuable tools for problem-solving and enhances our appreciation for the interconnectedness of mathematical concepts. The ability to efficiently find the LCM is not just a mathematical skill; it's a crucial tool for effective problem-solving across diverse domains.
Latest Posts
Latest Posts
-
1914 To 2024 How Many Years
May 13, 2025
-
80 Out Of 110 As A Percentage
May 13, 2025
-
Cuantos Dias Faltan Para El 17 De Agosto
May 13, 2025
-
How Many Hours To New Years
May 13, 2025
-
25 Ml Equals How Many Tablespoons
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 5 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.