What Is The Mass Of 0.560 Moles Of Chlorine Gas
Treneri
May 11, 2025 · 4 min read
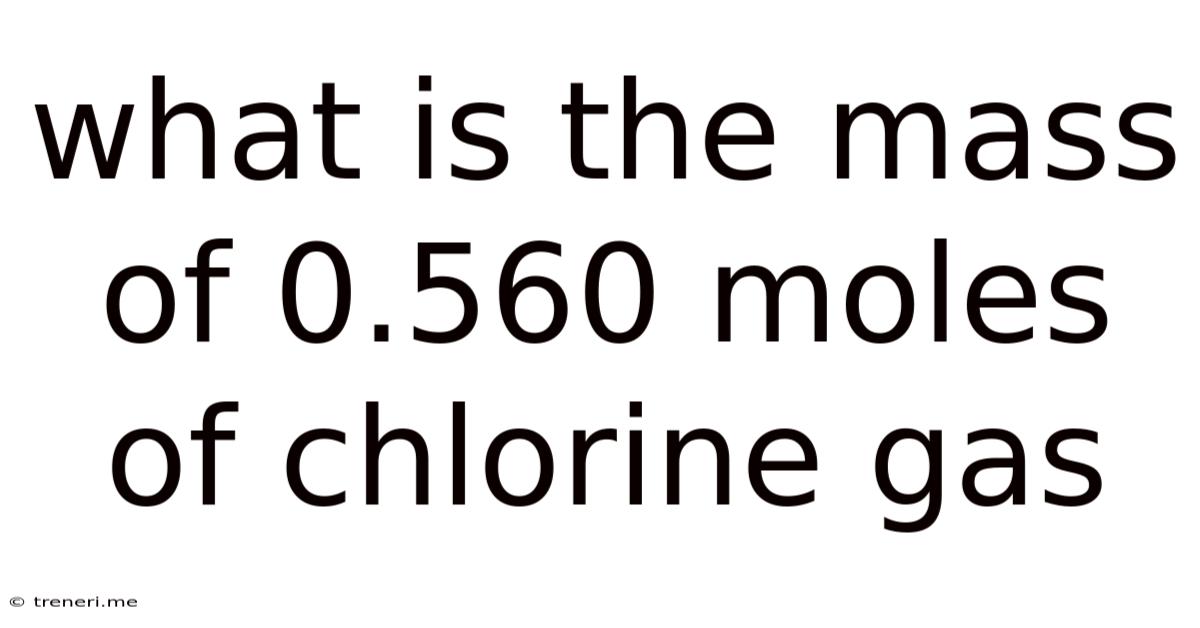
Table of Contents
What is the Mass of 0.560 Moles of Chlorine Gas? A Deep Dive into Molar Mass and Stoichiometry
Understanding the relationship between moles, molar mass, and mass is fundamental in chemistry. This article will guide you through calculating the mass of 0.560 moles of chlorine gas, explaining the concepts involved and providing a step-by-step solution. We'll also delve into the broader applications of molar mass calculations and stoichiometry in various chemical contexts.
Understanding Moles and Molar Mass
Before we tackle the calculation, let's clarify the key concepts:
What is a Mole?
A mole (mol) is a fundamental unit in chemistry representing Avogadro's number (approximately 6.022 x 10<sup>23</sup>) of particles. These particles can be atoms, molecules, ions, or any other specified entity. Think of it like a dozen (12) – a mole is just a much larger quantity. It provides a convenient way to work with incredibly large numbers of atoms or molecules in chemical reactions.
What is Molar Mass?
Molar mass is the mass of one mole of a substance. It's expressed in grams per mole (g/mol). For elements, the molar mass is numerically equal to the atomic mass (found on the periodic table) but with units of g/mol. For compounds, you need to sum the molar masses of all the constituent atoms.
Calculating the Molar Mass of Chlorine Gas (Cl₂)
Chlorine gas exists as a diatomic molecule, meaning two chlorine atoms are bonded together (Cl₂). To find its molar mass, we need to consider the atomic mass of chlorine from the periodic table. The atomic mass of chlorine is approximately 35.45 g/mol.
Therefore, the molar mass of Cl₂ is:
2 × 35.45 g/mol = 70.90 g/mol
Calculating the Mass of 0.560 Moles of Chlorine Gas
Now, we can use the following formula to calculate the mass:
Mass (g) = Moles (mol) × Molar Mass (g/mol)
Plugging in the values:
Mass (g) = 0.560 mol × 70.90 g/mol = 39.704 g
Therefore, the mass of 0.560 moles of chlorine gas is approximately 39.70 grams.
Beyond the Calculation: Applications of Molar Mass and Stoichiometry
The ability to convert between moles, mass, and molar mass is crucial for various chemical calculations and analyses. Here are some key applications:
1. Stoichiometry:
Stoichiometry is the quantitative study of reactants and products in chemical reactions. Molar mass is essential for converting between the masses of reactants and products, allowing us to determine the amounts of substances needed or produced in a reaction.
For instance, consider the reaction between hydrogen and oxygen to form water:
2H₂ + O₂ → 2H₂O
Knowing the molar masses of hydrogen, oxygen, and water, we can calculate the mass of water produced from a given mass of hydrogen or oxygen.
2. Solution Chemistry:
Molar mass is used to prepare solutions of a specific concentration. For example, to prepare a 1M (one molar) solution of sodium chloride (NaCl), you need to dissolve one mole of NaCl in one liter of solvent. Calculating the mass of NaCl required involves using its molar mass.
3. Gas Laws:
The ideal gas law (PV = nRT) relates the pressure (P), volume (V), number of moles (n), temperature (T), and the ideal gas constant (R) of a gas. Molar mass plays a critical role in determining the density of a gas, which is crucial in many applications.
4. Analytical Chemistry:
In quantitative analysis, molar mass is frequently used in titrations, gravimetric analysis, and other techniques to determine the concentration or amount of a substance in a sample.
5. Industrial Chemistry:
In industrial processes, accurate calculations using molar masses are vital for optimizing reaction yields, controlling product purity, and ensuring efficient resource utilization. This is crucial across various industries, including pharmaceuticals, fertilizers, and polymers.
Error Analysis and Significant Figures
It's important to pay attention to significant figures in calculations. In our example, 0.560 moles has three significant figures, and the molar mass of chlorine gas (70.90 g/mol) has four. Therefore, the final answer should also have three significant figures, which is why we reported the mass as 39.70 grams, not 39.704 grams.
Further Exploration: Isotopes and Atomic Mass
The atomic mass of an element listed on the periodic table is a weighted average of the masses of its isotopes. Isotopes are atoms of the same element with the same number of protons but a different number of neutrons. This weighted average accounts for the relative abundance of each isotope in nature. For very precise calculations, it's crucial to consider the isotopic composition of the element.
Conclusion
Calculating the mass of 0.560 moles of chlorine gas involved applying the fundamental concept of molar mass and the simple formula: Mass = Moles × Molar Mass. Understanding this relationship is a cornerstone of chemistry and is essential for a wide array of calculations in various chemical disciplines. This seemingly simple calculation opens the door to more complex stoichiometric problems, applications in solution chemistry, and a deeper understanding of the quantitative aspects of the chemical world. Mastering this concept is a crucial step in your chemical journey, paving the way for tackling more complex and challenging problems. Remember to always pay attention to significant figures and consider the potential impact of isotopic variations for high-precision work.
Latest Posts
Latest Posts
-
How Many Cups In 5 Gallons Of Water
May 12, 2025
-
What Is The Reciprocal Of 7 9
May 12, 2025
-
Find The Perimeter Of Equilateral Triangle
May 12, 2025
-
Cuanto Es 6 3 Pies En Centimetros
May 12, 2025
-
Greatest Common Factor Of 14 And 42
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Mass Of 0.560 Moles Of Chlorine Gas . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.