What Percent Is 120 Out Of 150
Treneri
May 13, 2025 · 5 min read
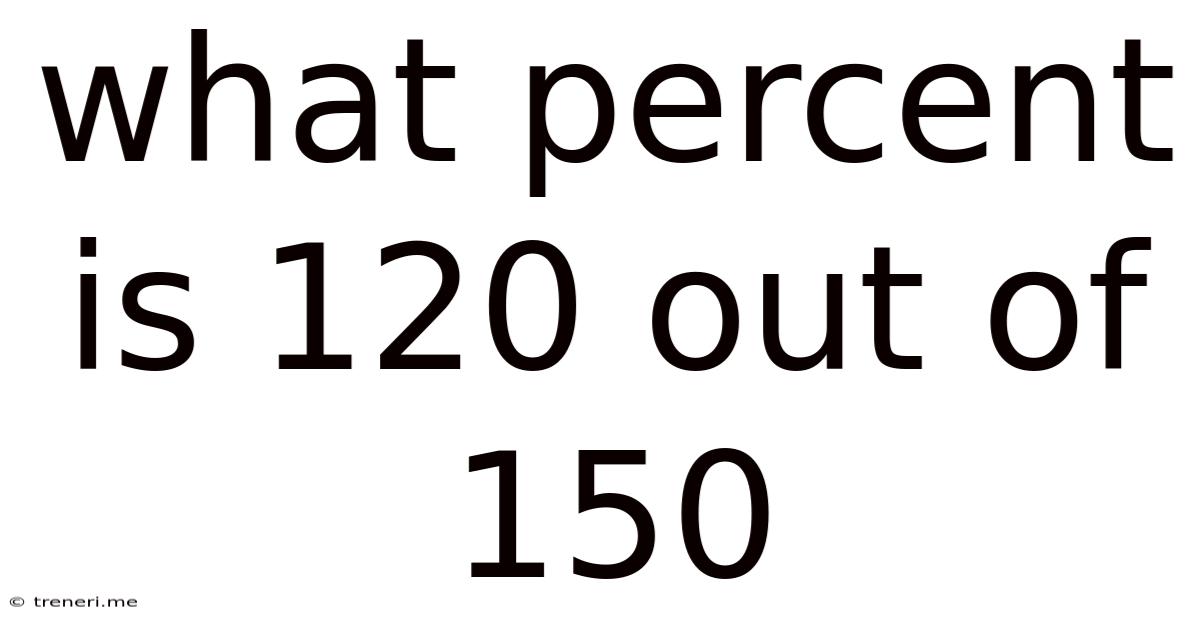
Table of Contents
What Percent is 120 out of 150? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with applications spanning various fields, from everyday budgeting and shopping to complex scientific analyses and financial modeling. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will delve into the calculation of what percentage 120 represents of 150, explaining the process step-by-step and exploring various related percentage problems. We’ll also touch upon the practical applications and significance of percentage calculations in real-world scenarios.
Understanding Percentages: The Basics
Before tackling the specific problem of determining what percentage 120 is of 150, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating the Percentage: 120 out of 150
To find what percentage 120 represents of 150, we follow a straightforward three-step process:
Step 1: Set up the Fraction
First, represent the problem as a fraction. The part (120) becomes the numerator, and the whole (150) becomes the denominator:
120/150
Step 2: Convert the Fraction to a Decimal
Next, divide the numerator (120) by the denominator (150):
120 ÷ 150 = 0.8
Step 3: Convert the Decimal to a Percentage
Finally, multiply the decimal by 100 to express it as a percentage:
0.8 x 100 = 80%
Therefore, 120 is 80% of 150.
Alternative Method: Using Proportions
An alternative method to calculate percentages involves using proportions. This method can be particularly helpful for solving more complex percentage problems. We can set up a proportion as follows:
Let x be the percentage we are trying to find.
x/100 = 120/150
To solve for x, we cross-multiply:
150x = 12000
Then, divide both sides by 150:
x = 12000 ÷ 150 = 80
Therefore, x = 80%, confirming our previous result.
Practical Applications of Percentage Calculations
The ability to calculate percentages is incredibly versatile and finds application in numerous real-world contexts. Here are just a few examples:
1. Finance and Budgeting:
- Calculating interest rates: Understanding interest rates, whether on loans or savings accounts, requires proficiency in percentage calculations.
- Determining discounts: Retailers frequently offer discounts expressed as percentages. Calculating the actual price reduction requires converting the percentage discount to a numerical value.
- Analyzing financial statements: Financial statements like income statements and balance sheets utilize percentages extensively to present data in a clear and concise manner. Profit margins, expense ratios, and debt-to-equity ratios are all expressed as percentages.
2. Science and Statistics:
- Presenting experimental results: Scientific studies often present data as percentages to showcase the proportion of successful outcomes or to compare different groups.
- Analyzing survey data: Surveys frequently use percentages to summarize responses and identify trends within the collected data.
- Calculating probabilities: Percentages are essential in expressing probabilities, providing a clear and easily understandable representation of the likelihood of an event occurring.
3. Everyday Life:
- Calculating tips: Calculating tips in restaurants is a common application of percentage calculations.
- Determining sales tax: Sales tax is typically expressed as a percentage of the purchase price.
- Understanding nutritional information: Food labels often express nutritional information, such as the percentage of daily recommended values for various nutrients, as percentages.
More Complex Percentage Problems: Variations and Extensions
While the example of 120 out of 150 is relatively straightforward, understanding percentages also involves tackling more complex scenarios. Let's explore some variations:
1. Finding the Whole when Given a Part and Percentage:
Imagine you know that 25% of a number is 50. How do you find the original number?
This requires rearranging the percentage formula. If we let 'x' be the whole number, we can set up the equation:
0.25x = 50
Solving for x, we get:
x = 50 ÷ 0.25 = 200
Therefore, the whole number is 200.
2. Finding the Percentage Increase or Decrease:
Calculating percentage changes is crucial for tracking trends and making comparisons. For instance, if a product's price increases from $100 to $120, the percentage increase is calculated as:
(120 - 100) / 100 x 100% = 20%
Conversely, if the price decreases from $120 to $100, the percentage decrease is:
(120 - 100) / 120 x 100% = 16.67%
Note the difference in the denominator when calculating a percentage decrease. We use the original value (120) as the base for the calculation.
3. Dealing with Multiple Percentages:
Sometimes, you might need to deal with multiple percentages in a single calculation. For example, finding the final price after successive discounts or tax additions requires careful attention to the order of operations.
Mastering Percentage Calculations: Tips and Tricks
- Practice regularly: The key to mastering any mathematical concept, including percentages, is consistent practice. Work through various examples, ranging from simple to more complex problems.
- Use a calculator: While it's beneficial to understand the underlying principles, using a calculator can streamline the calculation process, especially for more complex problems.
- Check your work: Always double-check your calculations to ensure accuracy. Even a small error can significantly impact the result.
- Visualize the problem: Sometimes, visualizing the problem as a fraction or a proportion can aid in understanding and solving the problem.
Conclusion: The Importance of Percentage Proficiency
The ability to calculate percentages accurately and efficiently is an invaluable skill across various aspects of life. From personal finance and budgeting to professional fields like science, statistics, and business, understanding percentages is essential for interpreting data, making informed decisions, and effectively communicating quantitative information. By mastering percentage calculations, you empower yourself to navigate a wide range of numerical challenges with confidence and precision. This guide has provided a thorough exploration of percentage calculations, addressing the specific problem of "what percent is 120 out of 150" and expanding upon it to cover more complex scenarios and applications. Remember to practice regularly, and you'll soon find yourself proficient in this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Round 26 To The Nearest Hundred
May 14, 2025
-
Cuantos Dias Faltan Para El 8 De Marzo
May 14, 2025
-
How Many Sides A Octagon Have
May 14, 2025
-
Odds Of 7 Heads In A Row
May 14, 2025
-
How Many Hours Till 6 00 Am
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 120 Out Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.