What Percent Is 16 Out Of 30
Treneri
May 12, 2025 · 4 min read
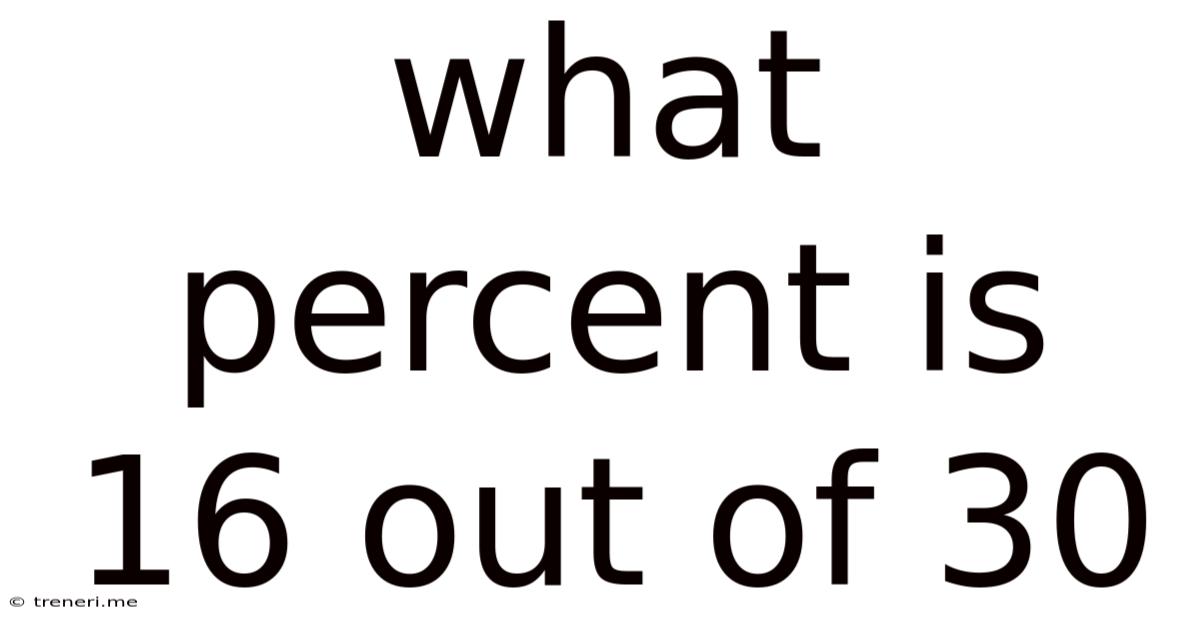
Table of Contents
What Percent is 16 out of 30? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life, from understanding sales discounts and interest rates to analyzing data and interpreting statistics. This comprehensive guide will delve into the process of determining what percent 16 out of 30 represents, exploring the underlying methodology and providing you with the tools to tackle similar percentage problems with confidence. We'll also explore practical applications and related concepts to solidify your understanding.
Understanding Percentages
Before we dive into the specifics of calculating 16 out of 30 as a percentage, let's establish a solid understanding of what percentages represent. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred," indicating the proportional relationship of a part to a whole.
For example, 50% means 50 out of 100, or one-half. Similarly, 25% means 25 out of 100, or one-quarter. Understanding this fundamental relationship is crucial for performing percentage calculations accurately.
Calculating the Percentage: Step-by-Step
To determine what percent 16 out of 30 is, we follow these simple steps:
Step 1: Formulate the Fraction:
First, express the given numbers as a fraction. In this case, 16 is the part and 30 is the whole. Therefore, the fraction is 16/30.
Step 2: Convert the Fraction to a Decimal:
To convert the fraction to a decimal, divide the numerator (16) by the denominator (30):
16 ÷ 30 = 0.5333...
Step 3: Convert the Decimal to a Percentage:
To convert the decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.5333... × 100 = 53.33...%
Therefore, 16 out of 30 is approximately 53.33%. The three dots (...) indicate that the decimal value is recurring (repeating infinitely). For practical purposes, rounding to two decimal places is usually sufficient.
Rounding and Precision
The result of 53.33% is an approximation. The decimal 0.5333... continues infinitely. The level of precision required depends on the context. In some cases, rounding to the nearest whole number (53%) may be sufficient, while in others, greater precision might be necessary (e.g., 53.33% or even more decimal places). Always consider the context of the problem to determine the appropriate level of rounding.
Alternative Calculation Method: Using Proportions
Another approach to solving this problem involves using proportions. We can set up a proportion to represent the relationship between the part (16), the whole (30), and the unknown percentage (x):
16/30 = x/100
To solve for x, cross-multiply:
30x = 1600
Divide both sides by 30:
x = 1600/30 = 53.33...%
This method yields the same result as the previous approach, reinforcing the accuracy of our calculation.
Practical Applications and Real-World Examples
Understanding percentage calculations is vital in numerous real-world scenarios:
-
Sales and Discounts: A store offers a 20% discount on an item. If the original price is $50, you can calculate the discount amount and the final price using percentages.
-
Interest Rates: Calculating simple or compound interest on loans or investments requires a solid grasp of percentage calculations.
-
Data Analysis: Percentages are frequently used to represent data proportions in charts, graphs, and reports. For example, you might express the percentage of students who passed an exam or the market share of a particular company.
-
Tax Calculations: Sales tax, income tax, and other taxes are often expressed as percentages.
-
Grade Calculations: In education, grades are often expressed as percentages, reflecting the proportion of correctly answered questions or completed assignments.
Expanding Your Understanding: Related Concepts
To further enhance your understanding of percentage calculations, consider exploring related concepts such as:
-
Percentage Increase and Decrease: These calculations involve determining the percentage change between two values. For example, finding the percentage increase in sales from one year to the next.
-
Percentage Points: Percentage points represent the difference between two percentages, not the percentage change. For instance, an increase from 10% to 15% is a 5-percentage point increase, but a 50% percentage increase.
-
Compound Interest: Understanding how interest accrues over time, including the compounding effect, is crucial in financial planning and investments.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill applicable across various aspects of life. By understanding the fundamental concepts and applying the step-by-step methods outlined in this guide, you can confidently tackle percentage problems, interpret data, and make informed decisions in various contexts. Remember to consider the context and choose the appropriate level of precision when rounding your results. Continuous practice and exploration of related concepts will further solidify your understanding and build your numerical literacy. This comprehensive guide provides a strong foundation for tackling even more complex percentage-related challenges.
Latest Posts
Latest Posts
-
How To Calculate Youngs Modulus From Stress Strain Graph
May 12, 2025
-
180 Days From January 22 2024
May 12, 2025
-
2 828 Rounded To The Nearest Hundredth
May 12, 2025
-
Born In 1978 How Old Am I
May 12, 2025
-
Round 89 To The Nearest Hundred
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 16 Out Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.