What Percent Is 2 Out Of 12
Treneri
May 10, 2025 · 4 min read
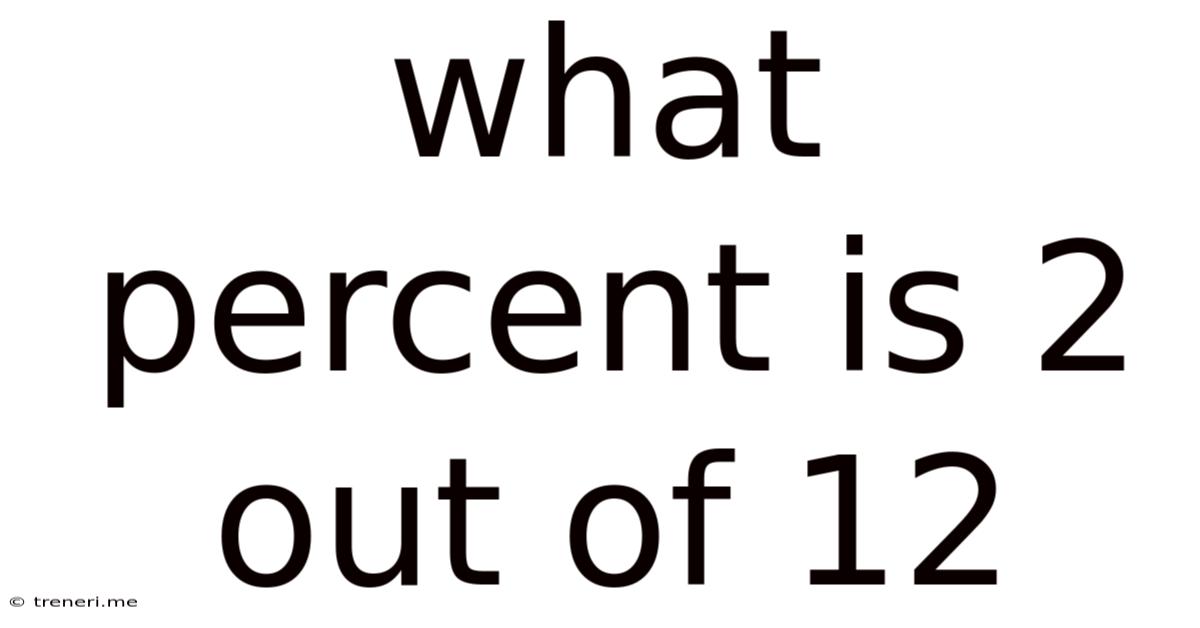
Table of Contents
What Percent is 2 out of 12? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and tips to analyzing data and understanding statistics. This comprehensive guide will delve into the question "What percent is 2 out of 12?" and explore the broader context of percentage calculations, offering practical examples and helpful tips along the way.
Calculating the Percentage: A Step-by-Step Approach
The question "What percent is 2 out of 12?" requires us to convert a fraction (2/12) into a percentage. Here's a step-by-step method:
Step 1: Convert the Fraction to a Decimal
To convert the fraction 2/12 to a decimal, we simply divide the numerator (2) by the denominator (12):
2 ÷ 12 = 0.166666...
We can round this decimal to a manageable number of decimal places. For our purposes, let's round to two decimal places: 0.17
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.17 x 100 = 17%
Therefore, 2 out of 12 is 17%. Note that we've rounded the decimal, so this is an approximation. The exact value, if expressed as a fraction, would be 16.67%.
Simplifying Fractions for Easier Calculation
Before diving into the decimal and percentage conversion, simplifying the fraction can make the calculation much easier. In this case, we can simplify 2/12 by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
2/12 = (2 ÷ 2) / (12 ÷ 2) = 1/6
Now, we can convert the simplified fraction 1/6 to a decimal:
1 ÷ 6 ≈ 0.1667
And then to a percentage:
0.1667 x 100 ≈ 16.67%
This shows that simplifying the fraction beforehand leads to a more precise result.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Let's consider some examples:
1. Sales and Discounts
Imagine a store offering a 20% discount on an item originally priced at $100. To calculate the discount amount, we multiply the original price by the percentage discount:
$100 x 0.20 = $20
The discount is $20, and the final price is $100 - $20 = $80.
2. Taxes and Tips
Calculating sales tax or service tips also involves percentages. If the sales tax is 6% on a $50 purchase, the tax amount is:
$50 x 0.06 = $3
The total cost, including tax, is $50 + $3 = $53.
Similarly, if you want to leave a 15% tip on a $75 dinner bill, the tip amount is:
$75 x 0.15 = $11.25
3. Data Analysis and Statistics
Percentages are frequently used in data analysis and statistics to represent proportions and trends. For example, if a survey shows that 20 out of 100 people prefer a particular brand, this can be expressed as 20% brand preference.
4. Financial Calculations
Percentages are fundamental to financial calculations, including interest rates, investment returns, and loan repayments. Understanding how percentages work is vital for making informed financial decisions.
Beyond the Basics: More Complex Percentage Problems
While the example of "What percent is 2 out of 12?" is relatively straightforward, percentage problems can become more complex. Let's explore some scenarios:
1. Finding the Original Value
Sometimes, you might know the percentage and the resulting value, and need to find the original value. For example, if a discounted price is $80 after a 20% discount, we can work backward to find the original price:
Let x be the original price. Then, 80% of x is $80:
0.80x = $80
x = $80 / 0.80 = $100
The original price was $100.
2. Percentage Increase or Decrease
Calculating percentage increase or decrease involves finding the difference between two values and expressing it as a percentage of the original value. For instance, if a stock price increased from $50 to $60, the percentage increase is:
((60 - 50) / 50) x 100 = 20%
3. Compound Interest
Compound interest calculations involve applying interest to both the principal amount and accumulated interest over time. This leads to exponential growth. Understanding compound interest is crucial for long-term financial planning.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering percentage calculations is consistent practice. Solve various problems to build your understanding and confidence.
-
Use a Calculator: Don't hesitate to use a calculator for complex calculations to ensure accuracy.
-
Understand the Concepts: Focus on understanding the underlying concepts, rather than just memorizing formulas.
-
Break Down Complex Problems: Divide complex percentage problems into smaller, manageable steps.
-
Check Your Work: Always check your answers to ensure accuracy.
Conclusion: The Importance of Percentages
Percentages are a powerful tool for understanding and expressing proportions and relationships between numbers. Mastering percentage calculations is an essential skill with wide-ranging applications in various fields. From simple everyday tasks to complex financial and statistical analyses, understanding percentages is crucial for making informed decisions and navigating the world around us. By understanding the fundamental principles and practicing regularly, you can build a strong foundation in percentage calculations and apply this valuable skill effectively in various contexts. Remember, even seemingly simple questions like "What percent is 2 out of 12?" can be a gateway to understanding more complex percentage-based problems.
Latest Posts
Latest Posts
-
How Many Ounces Is 2 2 3 Cups
May 11, 2025
-
Greatest Common Factor Of 48 And 84
May 11, 2025
-
What Is 66 Months In Years
May 11, 2025
-
3 25 Rounded To The Nearest Tenth
May 11, 2025
-
5 To The Power Of Negative 5
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 2 Out Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.