What Percent Is 5 Of 15
Treneri
May 11, 2025 · 4 min read
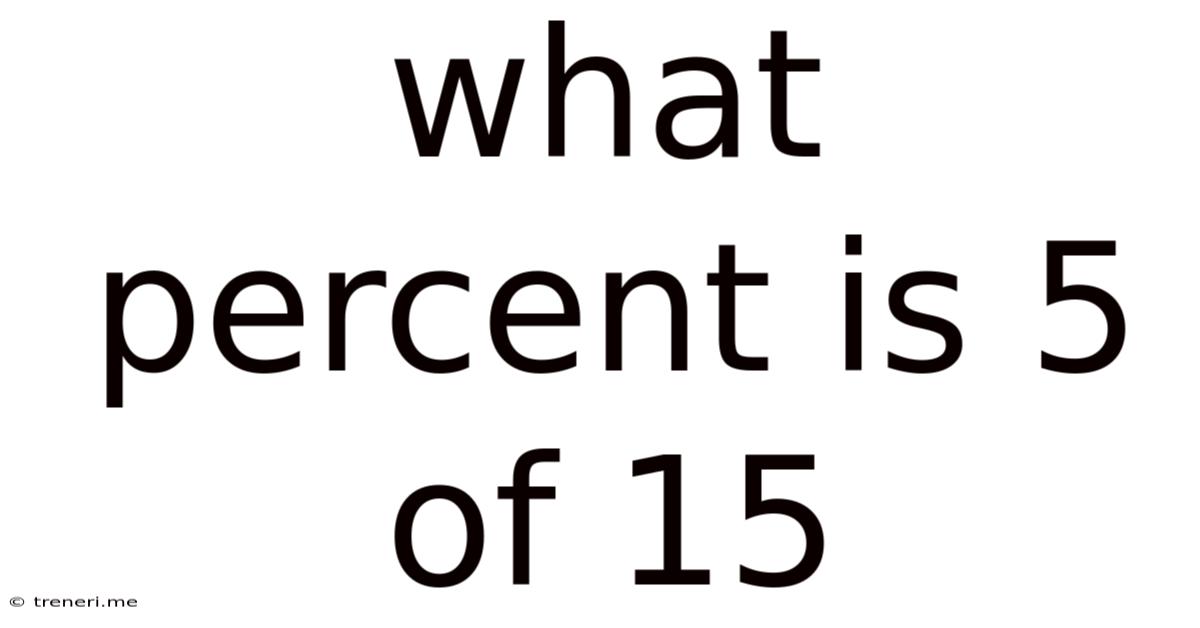
Table of Contents
What Percent is 5 of 15? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will explore the question, "What percent is 5 of 15?", providing a detailed explanation of the calculation process, offering multiple approaches, and highlighting practical applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" (from the Latin per centum). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Understanding this basic concept is key to solving percentage problems. To find what percent one number is of another, we essentially need to determine the ratio of the two numbers and express this ratio as a fraction of 100.
Calculating "What Percent is 5 of 15?"
There are several ways to solve this problem:
Method 1: Using the Proportion Method
This method involves setting up a proportion. We know that we want to find 'x' percent, where x is the unknown percentage. We can express this as a proportion:
- 5/15 = x/100
This proportion states that the ratio of 5 to 15 is equal to the ratio of x to 100. To solve for x, we cross-multiply:
- 15x = 500
Now, we divide both sides by 15:
-
x = 500/15
-
x ≈ 33.33
Therefore, 5 is approximately 33.33% of 15.
Method 2: Using Decimal Conversion
This method involves first converting the fraction 5/15 to a decimal and then multiplying by 100 to express it as a percentage.
-
Simplify the Fraction: The fraction 5/15 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 5. This simplifies to 1/3.
-
Convert to Decimal: To convert the fraction 1/3 to a decimal, we perform the division: 1 ÷ 3 ≈ 0.3333
-
Convert to Percentage: To express this decimal as a percentage, we multiply by 100: 0.3333 × 100 ≈ 33.33%
Therefore, 5 is approximately 33.33% of 15.
Method 3: Using a Calculator
Most calculators have a percentage function. You can simply input the equation: (5/15)*100 to directly obtain the result: 33.33%. This is the quickest and most efficient method for straightforward calculations.
Real-World Applications
Understanding percentage calculations is invaluable in numerous real-world situations. Here are a few examples:
1. Sales and Discounts:
Imagine a store is offering a 20% discount on a $15 item. To calculate the discount amount, you would find 20% of $15: (20/100) * $15 = $3. The sale price would be $15 - $3 = $12.
2. Taxes and Tips:
Calculating sales tax or a restaurant tip involves similar percentage calculations. If the sales tax is 6%, and your purchase is $50, the tax amount would be (6/100) * $50 = $3.
3. Grade Calculations:
In educational settings, percentages are used extensively to represent grades. If you scored 12 out of 15 on a quiz, your percentage score would be (12/15) * 100 = 80%.
4. Financial Analysis:
Percentage changes are crucial for analyzing financial data. If a stock's price increased from $10 to $12, the percentage increase would be [(12-10)/10] * 100 = 20%.
5. Scientific Research:
In scientific research, percentages are used to represent proportions and changes in various phenomena. For instance, in clinical trials, the success rate of a new drug might be expressed as a percentage.
Beyond the Basics: Dealing with More Complex Scenarios
While the example of "What percent is 5 of 15?" is relatively simple, the principles can be extended to more complex situations. Consider these scenarios:
-
Finding the whole: If you know that 25% of a number is 10, you can set up a proportion to find the whole number: 25/100 = 10/x. Solving for x gives you the original number.
-
Finding the part: If you know the whole and the percentage, you can calculate the part. For instance, finding 15% of 80 involves calculating (15/100) * 80.
-
Percentage increase/decrease: Calculating percentage changes requires understanding the difference between the new value and the original value, then dividing by the original value, and finally multiplying by 100.
Conclusion
Understanding how to calculate percentages is an essential life skill. The seemingly simple question, "What percent is 5 of 15?" highlights the fundamental concepts and opens the door to solving more complex percentage problems in various contexts. Mastering this skill enhances your ability to interpret data, make informed decisions, and successfully navigate numerous aspects of daily life and professional endeavors. By employing the methods outlined above—proportion, decimal conversion, and calculator use—you'll be well-equipped to tackle any percentage calculation you encounter. Remember to always double-check your work and consider the context of the problem to ensure your answer is accurate and meaningful.
Latest Posts
Latest Posts
-
What Grade Is A 28 Out Of 30
May 13, 2025
-
Unknown Leg Lengths In Right Triangles
May 13, 2025
-
Cuantos Litros Tiene Un Cuarto De Galon
May 13, 2025
-
Greatest Common Factor Of 30 And 80
May 13, 2025
-
60 Days From June 19 2024
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 5 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.