What Percent Is 78 Of 120
Treneri
May 09, 2025 · 4 min read
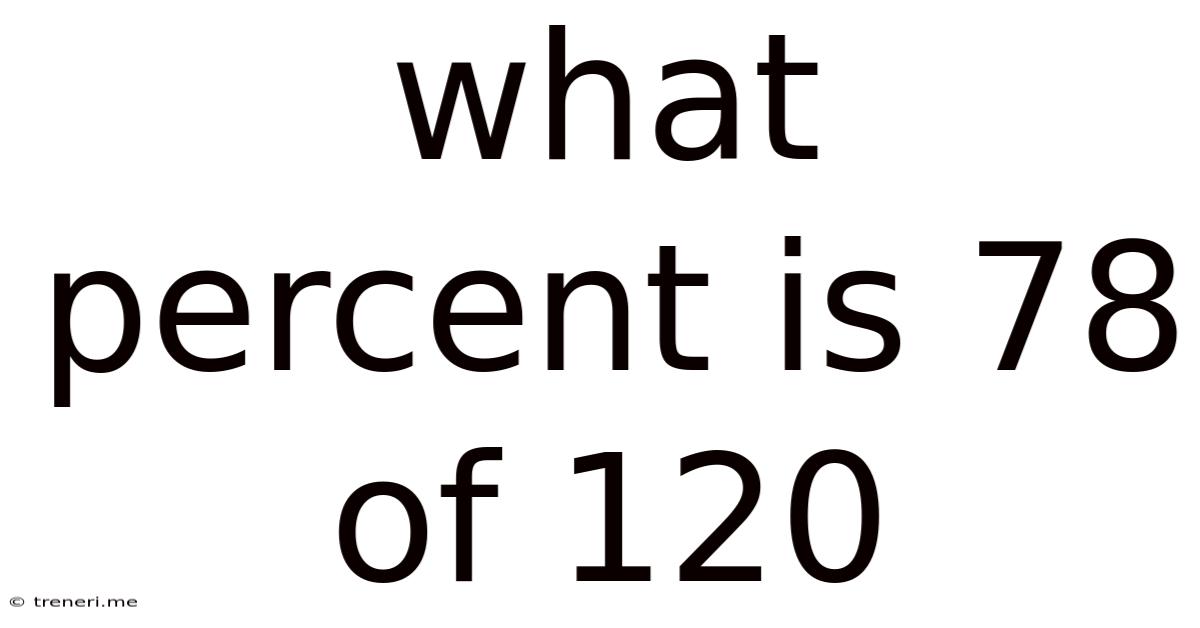
Table of Contents
What Percent is 78 of 120? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex statistical analysis and scientific research. Understanding how to determine what percentage one number represents of another is crucial for interpreting data, making informed decisions, and solving various problems. This comprehensive guide will delve into the calculation of "What percent is 78 of 120?", explaining the process step-by-step and exploring related percentage concepts.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5 in decimal form.
Calculating "What Percent is 78 of 120?"
To determine what percentage 78 represents of 120, we need to follow these simple steps:
Step 1: Set up the Fraction
First, express the relationship between the two numbers as a fraction. The part (78) will be the numerator, and the whole (120) will be the denominator:
78/120
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (78) by the denominator (120):
78 ÷ 120 = 0.65
Step 3: Convert the Decimal to a Percentage
To express the decimal as a percentage, multiply the decimal by 100 and add the percent sign (%):
0.65 x 100 = 65%
Therefore, 78 is 65% of 120.
Alternative Calculation Method: Using Proportions
Another approach to solving this problem involves using proportions. A proportion is an equation stating that two ratios are equal. We can set up a proportion to find the unknown percentage (x):
x/100 = 78/120
To solve for x, we can cross-multiply:
120x = 7800
Then, divide both sides by 120:
x = 7800 ÷ 120 = 65
Therefore, x = 65%, confirming our previous result.
Practical Applications of Percentage Calculations
Understanding percentage calculations has widespread practical applications:
1. Sales and Discounts:
Retailers frequently advertise sales and discounts using percentages. For example, a "25% off" sale means the price is reduced by 25% of the original price. Knowing how to calculate percentages helps consumers determine the actual savings and the final price.
2. Finance and Investing:
Percentage calculations are essential in finance and investing. Interest rates, returns on investments, and financial ratios are all expressed as percentages. Understanding these percentages is critical for making informed financial decisions.
3. Statistics and Data Analysis:
Percentages are widely used in statistics to represent proportions and probabilities. For instance, survey results are often presented as percentages to show the distribution of responses. Analyzing these percentages helps researchers draw conclusions and make predictions.
4. Scientific Research:
In scientific research, percentages are used to express the concentration of solutions, the success rate of experiments, and the prevalence of certain phenomena. Accurate percentage calculations are crucial for ensuring the validity and reliability of scientific findings.
Beyond the Basics: Advanced Percentage Concepts
While calculating "what percent is 78 of 120" provides a fundamental understanding of percentages, let's explore some more advanced concepts:
1. Percentage Increase and Decrease:
Calculating percentage increases and decreases is crucial for analyzing changes over time. For example, if a quantity increases from 100 to 120, the percentage increase is calculated as:
[(120 - 100) / 100] x 100% = 20%
Similarly, a decrease from 120 to 100 would represent a 16.67% decrease.
2. Percentage Points vs. Percentage Change:
It's important to distinguish between percentage points and percentage change. A percentage point refers to the absolute difference between two percentages, while percentage change refers to the relative difference. For example, an increase from 20% to 30% represents a 10 percentage point increase, but a 50% percentage increase.
3. Compounding Percentages:
Compounding percentages involve calculating percentages on top of previous percentages. This is commonly seen in interest calculations where interest earned is added to the principal amount, and subsequent interest is calculated on the larger amount.
4. Using Percentages in Spreadsheets and Software:
Spreadsheet software like Microsoft Excel and Google Sheets provide built-in functions for percentage calculations, simplifying the process and allowing for efficient data analysis.
Error Handling and Accuracy
When working with percentages, maintaining accuracy is vital. Rounding errors can accumulate, leading to significant inaccuracies in complex calculations. It's recommended to use as many decimal places as possible during intermediate calculations and round only the final result to the desired level of precision.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages accurately and efficiently is a valuable skill across numerous disciplines. Understanding the fundamental concepts, including converting fractions to decimals and percentages, using proportions, and applying percentages to real-world scenarios, empowers individuals to interpret data, make informed decisions, and solve a wide range of problems. By mastering these techniques, you can confidently tackle various percentage-related challenges and enhance your analytical abilities. The seemingly simple calculation of "What percent is 78 of 120?" serves as a springboard to explore a much broader world of percentage applications and their significant impact on daily life and professional endeavors. This comprehensive guide provides a solid foundation for further exploration and deeper understanding of this crucial mathematical concept.
Latest Posts
Latest Posts
-
How Many Days Is 229 Hours
May 09, 2025
-
How Much Longer Till 1 Pm
May 09, 2025
-
Si Naci En 1963 Cuantos Anos Tengo En El 2023
May 09, 2025
-
Find Shortest Distance From Point To Plane
May 09, 2025
-
4000 Bce Is How Many Years Ago
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 78 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.