What Percent Is Equivalent To 7/50
Treneri
May 14, 2025 · 4 min read
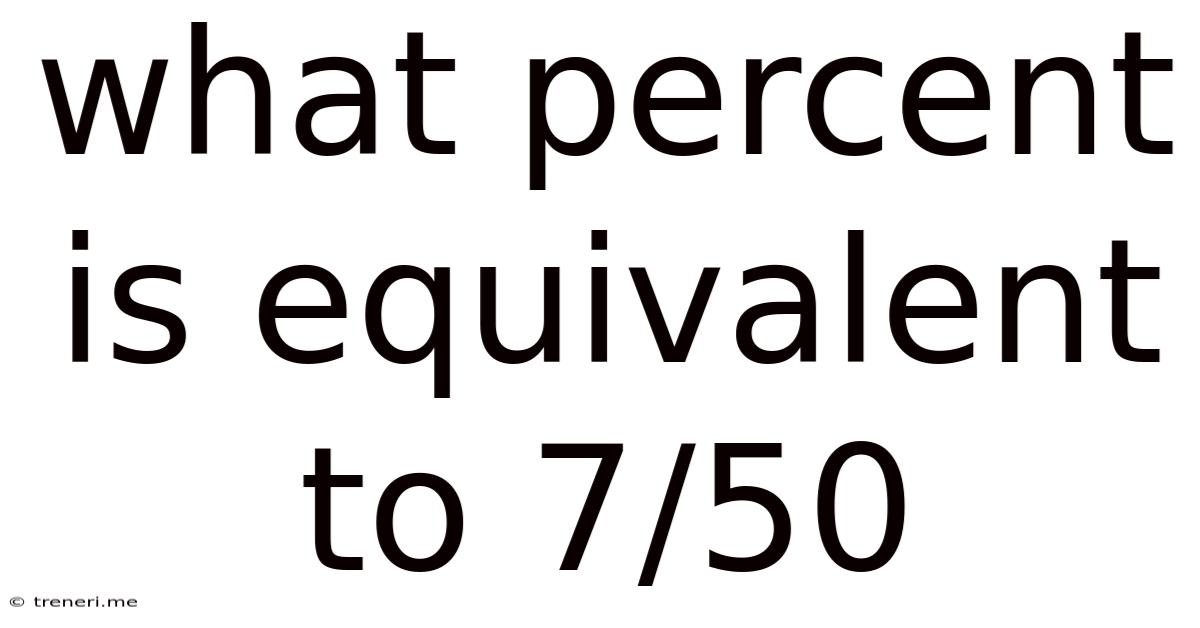
Table of Contents
What Percent is Equivalent to 7/50? A Comprehensive Guide to Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding statistical data and financial reports. This comprehensive guide will delve into the process of converting the fraction 7/50 to a percentage, providing a step-by-step explanation and exploring related concepts to solidify your understanding. We'll also look at practical examples and explore different methods for tackling similar fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, 7/50 means we have 7 parts out of a total of 50 equal parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." For example, 50% means 50 out of 100, or 50/100.
Converting 7/50 to a Percentage: The Step-by-Step Method
The most straightforward method for converting a fraction to a percentage involves two simple steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator:
7 ÷ 50 = 0.14
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%):
0.14 x 100 = 14%
Therefore, 7/50 is equivalent to 14%.
Alternative Methods for Fraction-to-Percentage Conversion
While the above method is the most common, there are other approaches you can use, especially if you're comfortable working with equivalent fractions.
Method 1: Finding an Equivalent Fraction with a Denominator of 100
Since a percentage is a fraction out of 100, we can try to find an equivalent fraction for 7/50 with a denominator of 100. To do this, we ask ourselves: what number multiplied by 50 equals 100? The answer is 2.
So, we multiply both the numerator and the denominator of 7/50 by 2:
(7 x 2) / (50 x 2) = 14/100
Since 14/100 means 14 out of 100, this is equivalent to 14%.
Method 2: Using Proportions
We can set up a proportion to solve for the percentage:
7/50 = x/100
To solve for x (the percentage), cross-multiply:
50x = 700
x = 700/50
x = 14
Therefore, 7/50 is equivalent to 14%.
Practical Applications and Real-World Examples
Understanding fraction-to-percentage conversions is crucial in various real-world scenarios:
-
Discounts: If a store offers a 14% discount on an item, you can easily calculate the discount amount by multiplying the original price by 0.14 (or 14/100).
-
Taxes: Sales tax is often expressed as a percentage. Knowing how to convert fractions to percentages allows you to calculate the tax amount on a purchase.
-
Surveys and Statistics: Survey results are frequently presented as percentages. Understanding how percentages are derived from fractions is essential for interpreting data correctly.
-
Financial Calculations: Interest rates, investment returns, and many other financial calculations involve percentages.
-
Baking and Cooking: Recipes often require fractions of ingredients. Converting these fractions to percentages can be useful for scaling recipes up or down.
Expanding Your Understanding: Working with More Complex Fractions
The methods described above can be applied to more complex fractions as well. Let's consider an example: converting 17/25 to a percentage.
Step 1: Convert to Decimal: 17 ÷ 25 = 0.68
Step 2: Convert to Percentage: 0.68 x 100 = 68%
Therefore, 17/25 is equivalent to 68%. You can also apply the equivalent fraction method or the proportion method to reach the same result. Remember to always divide the numerator by the denominator first to obtain the decimal representation.
Troubleshooting Common Mistakes
-
Incorrect Order of Operations: When converting a fraction to a decimal, ensure you divide the numerator by the denominator, not the other way around.
-
Forgetting the Percentage Sign: Always remember to include the "%" symbol when expressing your final answer as a percentage.
-
Decimal Point Errors: Be careful when multiplying by 100 to convert from decimal to percentage. Ensure you're moving the decimal point two places to the right correctly.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a vital mathematical skill with numerous real-world applications. This guide has provided a detailed explanation of the process, along with alternative methods and practical examples. By mastering this skill, you'll be better equipped to tackle various problems involving percentages, improving your analytical and problem-solving abilities in diverse fields. Remember to practice regularly and apply these concepts in different scenarios to solidify your understanding and build confidence. Consistent practice will make fraction-to-percentage conversions second nature. Furthermore, understanding this fundamental conversion enhances your ability to interpret data effectively, make informed decisions, and navigate various quantitative situations with ease.
Latest Posts
Latest Posts
-
How Many Miles Does 10 Of Gas Get You
May 14, 2025
-
452 Rounded To The Nearest Hundred
May 14, 2025
-
How Much Is 20 Of 400 000
May 14, 2025
-
What Is 8 Cm In Ring Size
May 14, 2025
-
85 Rounded To The Nearest 10
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is Equivalent To 7/50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.