What Percent Of 12 Is 7
Treneri
May 11, 2025 · 4 min read
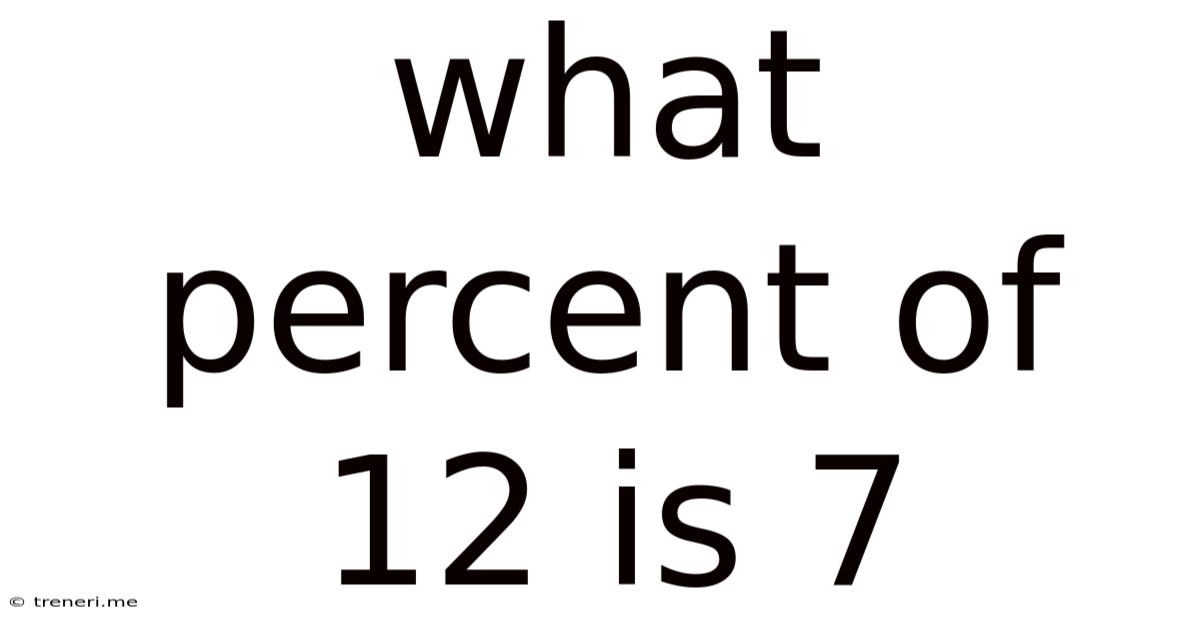
Table of Contents
What Percent of 12 is 7? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and interpreting statistics. This article will delve into the question, "What percent of 12 is 7?", providing a step-by-step solution, exploring different methods for calculating percentages, and demonstrating the practical relevance of this seemingly simple calculation. We'll also cover related percentage problems and provide you with the tools to confidently tackle similar questions in the future.
Understanding the Problem: What Percent of 12 is 7?
The core of this problem lies in determining the ratio of 7 to 12, expressed as a percentage. In simpler terms, we need to find what fraction of 12 is represented by 7, and then convert that fraction into a percentage. Percentage, as you know, means "per hundred," or parts out of 100.
Method 1: The Formula Approach
The most direct approach involves using the basic percentage formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 7
- Whole: 12
Therefore, the calculation becomes:
(7 / 12) * 100 = Percentage
Let's break it down:
-
Divide the part by the whole: 7 / 12 ≈ 0.5833
-
Multiply the result by 100: 0.5833 * 100 ≈ 58.33
Therefore, 7 is approximately 58.33% of 12.
Method 2: Using Proportions
Another effective method utilizes proportions. We can set up a proportion to solve for the unknown percentage (let's call it 'x'):
7/12 = x/100
To solve for 'x', we cross-multiply:
12x = 700
Now, divide both sides by 12:
x = 700 / 12 ≈ 58.33
Again, we arrive at the answer: 7 is approximately 58.33% of 12.
Method 3: The Decimal Approach
This method involves converting the fraction to a decimal and then multiplying by 100. Following the same logic as before:
-
Convert the fraction to a decimal: 7/12 ≈ 0.5833
-
Multiply by 100 to express as a percentage: 0.5833 * 100 ≈ 58.33%
This method is particularly useful when working with calculators or spreadsheets.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is incredibly useful in many real-world scenarios. Here are a few examples:
-
Discounts: If a store offers a 20% discount on an item originally priced at $12, you can use percentage calculations to determine the discount amount ($2.40) and the final price ($9.60).
-
Taxes: Calculating sales tax or income tax often involves working with percentages. For instance, if the sales tax is 6%, you can calculate the tax amount on a purchase and the total cost.
-
Tips: Determining the appropriate tip amount in a restaurant usually involves calculating a percentage of the bill.
-
Grade Calculation: In education, your final grade is often calculated as a weighted average of different assignments or tests, each carrying a certain percentage weight.
-
Data Analysis: Percentages are vital in data analysis, allowing for easy comparison of proportions across different data sets. For example, comparing the percentage of men and women in a particular profession.
-
Finance: Percentages are crucial in various financial applications, such as calculating interest rates, returns on investment, and loan payments.
Related Percentage Problems and Solutions
Let's explore some related problems to further solidify your understanding:
Problem 1: What percent of 15 is 9?
Using the formula: (9/15) * 100 = 60%
Problem 2: 25% of what number is 10?
Let the number be 'x'. Then: (25/100) * x = 10. Solving for x, we get x = 40.
Problem 3: What is 150% of 20?
(150/100) * 20 = 30
Tips for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering any mathematical skill is consistent practice. Try solving different percentage problems regularly.
-
Use Different Methods: Experiment with all the methods discussed (formula, proportions, decimal) to find the approach that suits you best.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles of percentages and ratios.
-
Utilize Online Resources: There are numerous online resources, tutorials, and calculators available to help you practice and learn more about percentages.
-
Break Down Complex Problems: If faced with a more complex percentage problem, break it down into smaller, manageable steps.
Conclusion: Beyond the Numbers
While this article focused on the specific calculation of what percent of 12 is 7 (approximately 58.33%), the real takeaway is a broader understanding of percentage calculations and their ubiquitous applications. Mastering this skill provides a powerful tool for navigating various aspects of daily life, from personal finance to professional pursuits. By understanding the methods, practicing regularly, and applying the concepts in real-world contexts, you'll build confidence and proficiency in this fundamental area of mathematics. Remember, percentage calculations are more than just numbers; they're tools that empower you to understand and interpret data more effectively.
Latest Posts
Latest Posts
-
What Is The Multiplicative Inverse Of 1 2
May 13, 2025
-
30 Days From December 8 2023
May 13, 2025
-
Greatest Common Factor Of 26 And 14
May 13, 2025
-
How Much Is 20 Stones In Pounds
May 13, 2025
-
How To Find Youngs Modulus From Stress Strain Curve
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 12 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.