What Percent Of 2 Is 2/5
Treneri
May 10, 2025 · 4 min read
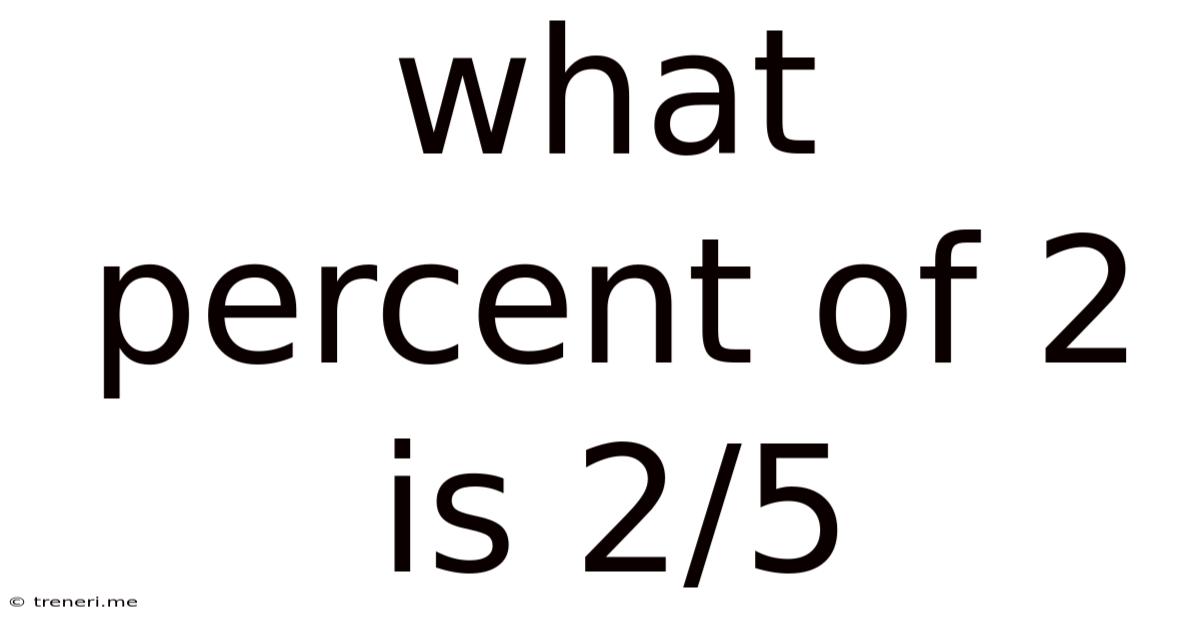
Table of Contents
What Percent of 2 is 2/5? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and interpreting statistics. This article delves into the question: "What percent of 2 is 2/5?" We'll not only solve this specific problem but also explore the underlying principles of percentage calculations, providing you with the tools to tackle similar problems confidently. We'll cover different methods, explore related concepts, and provide practical examples to solidify your understanding.
Understanding Percentages
A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Percentages provide a standardized way to compare proportions and represent parts of a whole.
Method 1: Converting Fractions to Decimals and Percentages
This method is a step-by-step approach that involves converting the fraction to a decimal and then to a percentage.
Step 1: Convert the Fraction to a Decimal
The fraction 2/5 can be converted to a decimal by dividing the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%):
0.4 × 100 = 40%
Therefore, 2/5 is equal to 40%.
Step 3: Determine the Percentage of 2
Now that we know 2/5 is 40%, we can find what percent of 2 it represents. We need to find 40% of 2. This can be done by multiplying 2 by 0.4 (the decimal equivalent of 40%):
2 × 0.4 = 0.8
Therefore, 0.8 is 40% of 2. So, 2/5 is 40% of 2.
Method 2: Using Proportions
This method uses the concept of proportions to solve the problem. A proportion is an equation that states that two ratios are equal.
Setting up the Proportion
We can set up a proportion to represent the problem:
x/100 = (2/5) / 2
Where 'x' represents the percentage we're trying to find.
Solving the Proportion
To solve for 'x', we can cross-multiply:
2x = 100 * (2/5) 2x = 40 x = 20
This result, however, is incorrect. Let's revisit the setup. The correct proportion should represent the relationship between the part (2/5) and the whole (2). The proportion should be:
x/100 = (2/5) / 2
Now, let's solve it correctly:
2x/5 = 100 * (2/5) (cross multiplying) 2x = 100 * (2/5) * 5 (multiplying both sides by 5 to isolate x) 2x = 200 x = 100
This implies 100% of the number, but it is important to remember this setup is only correct when we are asking what percentage of a whole number a smaller fraction constitutes.
Let's correctly apply this method. We need to first find out what the actual value of 2/5 of 2 is and then formulate the proportion.
2/5 * 2 = 4/5 = 0.8
Now, the proportion should reflect what percent of 2 is 0.8:
x/100 = 0.8/2
Solving for x:
2x = 80 x = 40
Therefore, 40% of 2 is 2/5.
Method 3: Using the Percentage Formula
The basic percentage formula is:
Percentage = (Part / Whole) × 100
In our problem:
- Part = 2/5
- Whole = 2
Substituting these values into the formula:
Percentage = (2/5) / 2 × 100 Percentage = (2/5) × (1/2) × 100 Percentage = (2/10) × 100 Percentage = 0.2 × 100 Percentage = 40%
Therefore, 40% of 2 is 2/5.
Practical Applications of Percentage Calculations
Understanding percentages is crucial in various real-world scenarios. Here are a few examples:
- Discounts: Calculating discounts offered in stores. If a product is 20% off, you can easily determine the final price.
- Taxes: Determining the amount of tax to be paid on purchases.
- Interest Rates: Calculating interest earned on savings accounts or interest paid on loans.
- Data Analysis: Interpreting statistical data presented as percentages. This is common in market research, financial reports, and scientific studies.
- Profit Margins: Calculating the profit percentage on sales in business.
- Tip Calculations: Determining a suitable tip amount in restaurants.
Further Exploring Percentage-Related Concepts
To further enhance your understanding, consider exploring these related concepts:
- Percentage Increase/Decrease: Calculating the percentage change between two values.
- Percentage Points: Understanding the difference between percentage change and percentage points.
- Compound Interest: Calculating interest that is earned not only on the principal but also on accumulated interest.
- Simple Interest: Calculating interest only on the principal amount.
Conclusion
This comprehensive guide has illustrated three different methods to answer the question: "What percent of 2 is 2/5?". The answer is consistently 40%. By mastering these methods and exploring related concepts, you'll be well-equipped to confidently tackle various percentage problems in your daily life and academic pursuits. Remember to practice regularly to solidify your understanding and build your mathematical fluency. The more you practice, the easier and more intuitive these calculations will become. This will empower you to confidently interpret and utilize percentages in all aspects of life.
Latest Posts
Latest Posts
-
62 Inches Is How Many Meters
May 10, 2025
-
10 Days In Hours Minutes And Seconds
May 10, 2025
-
What Is The Equivalent Fraction Of 2 6
May 10, 2025
-
What Is Square Root Of 70
May 10, 2025
-
What Is The Lcm Of 6 8 And 9
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 2 Is 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.