What Percent Of 250 Is 200
Treneri
May 10, 2025 · 4 min read
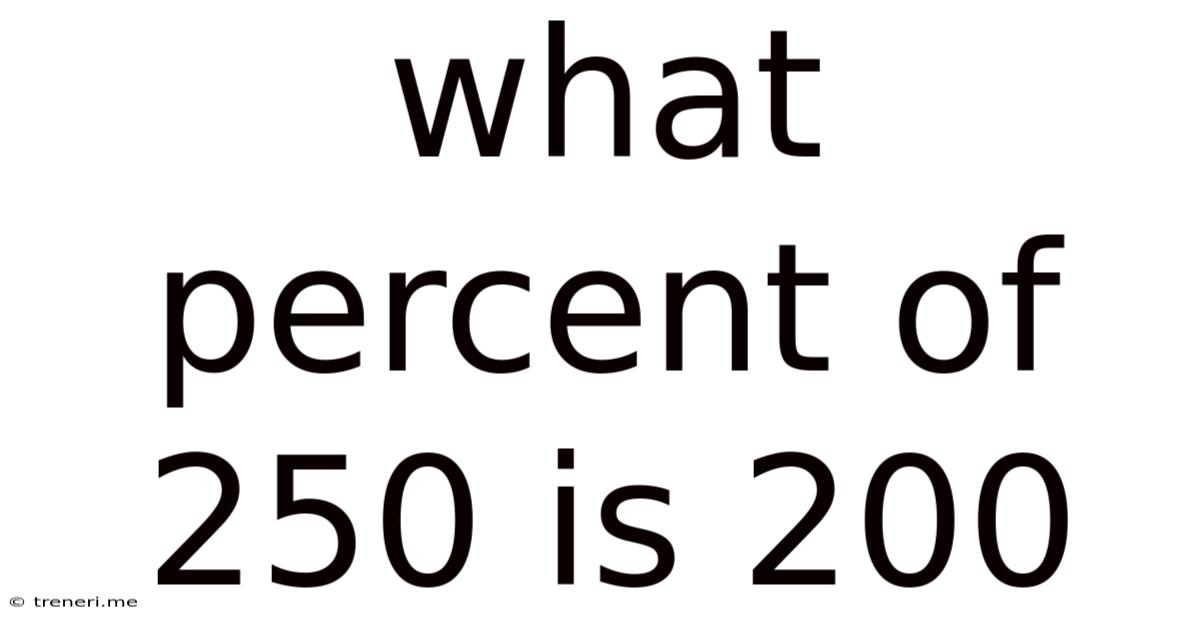
Table of Contents
What Percent of 250 is 200? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to analyzing data and understanding financial reports. This article delves into the question, "What percent of 250 is 200?", providing a step-by-step solution, exploring different calculation methods, and showcasing the practical relevance of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote percentage. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used to represent proportions, changes, and comparisons in a readily understandable way.
Calculating "What Percent of 250 is 200?"
The core question, "What percent of 250 is 200?", requires us to find the percentage that 200 represents when compared to 250. We can solve this using several methods:
Method 1: Using the Formula
The most straightforward method involves a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 200
- Whole: 250
Substituting the values into the formula:
(200 / 250) * 100% = 80%
Therefore, 200 is 80% of 250.
Method 2: Setting up a Proportion
Another approach is to set up a proportion:
x/100 = 200/250
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
250x = 20000
x = 20000 / 250
x = 80
Therefore, x = 80%, confirming that 200 is 80% of 250.
Method 3: Using Decimal Conversion
This method involves converting the fraction 200/250 into a decimal and then multiplying by 100%:
200 / 250 = 0.8
0.8 * 100% = 80%
Again, we arrive at the conclusion that 200 is 80% of 250.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in many real-world scenarios:
1. Retail and Sales
- Discounts: Stores frequently advertise discounts like "20% off." Calculating the actual price reduction requires percentage calculations. For example, a $100 item with a 20% discount will cost $80 ($100 * 0.8 = $80).
- Sales Tax: Sales tax is added to the price of goods and services. Calculating the final price, including tax, requires adding the tax percentage to the base price.
- Profit Margins: Businesses use percentage calculations to determine their profit margin—the difference between the cost of goods and the selling price.
2. Finance
- Interest Rates: Interest rates on loans and investments are expressed as percentages. Calculating the total interest paid or earned involves percentage calculations.
- Investment Returns: Investors track the percentage return on their investments to assess their performance.
- Inflation: Inflation, the rate at which prices increase, is expressed as a percentage, affecting purchasing power and economic planning.
3. Data Analysis and Statistics
- Data Representation: Percentages are frequently used to represent data in charts and graphs, making it easier to visualize proportions and trends.
- Statistical Analysis: Percentage changes are used to compare data sets over time or across different groups.
4. Everyday Life
- Tipping: Calculating a tip in a restaurant typically involves determining a percentage of the bill.
- Grading: Grades in many educational systems are often expressed as percentages.
Advanced Percentage Calculations
While the example "What percent of 250 is 200?" is straightforward, percentage calculations can become more complex. Here are some advanced scenarios:
1. Finding the Whole when given the Percentage and Part
If you know that 20% of a number is 50, you can find the whole number using the following formula:
Whole = (Part / Percentage) * 100
In this case:
Whole = (50 / 20) * 100 = 250
Therefore, 250 is the whole number.
2. Finding the Part when given the Percentage and Whole
If you know that 15% of 300 is needed, the calculation is:
Part = (Percentage / 100) * Whole
Part = (15/100) * 300 = 45
Therefore, 15% of 300 is 45.
3. Percentage Increase and Decrease
Percentage increase or decrease is calculated by finding the difference between two values and then expressing that difference as a percentage of the original value.
For example, if a value increases from 100 to 120, the percentage increase is:
((120 - 100) / 100) * 100% = 20%
Similarly, a decrease from 150 to 120 would represent a:
((150 - 120) / 150) * 100% = 20% decrease.
Conclusion
Understanding percentages is a critical life skill with far-reaching applications. This article thoroughly explored how to calculate "What percent of 250 is 200?", detailing multiple methods and showcasing the practical uses of percentage calculations in various fields, from retail and finance to data analysis and everyday life. Mastering percentage calculations empowers individuals to make informed decisions, analyze data effectively, and navigate the numerical aspects of our world with greater confidence. The ability to quickly and accurately calculate percentages is a valuable asset in both personal and professional settings. By understanding the underlying principles and practicing different calculation methods, you can confidently tackle any percentage problem you encounter.
Latest Posts
Latest Posts
-
Convert Kinematic Viscosity To Dynamic Viscosity
May 10, 2025
-
What Is 90 Days From August 12
May 10, 2025
-
Dress Size By Height And Weight
May 10, 2025
-
How Much Does A Fluid Ounce Of Breast Milk Weigh
May 10, 2025
-
How Many Gallons In A 40 X 20 Pool
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 250 Is 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.