What Percent Of 30 Is 10
Treneri
May 11, 2025 · 4 min read
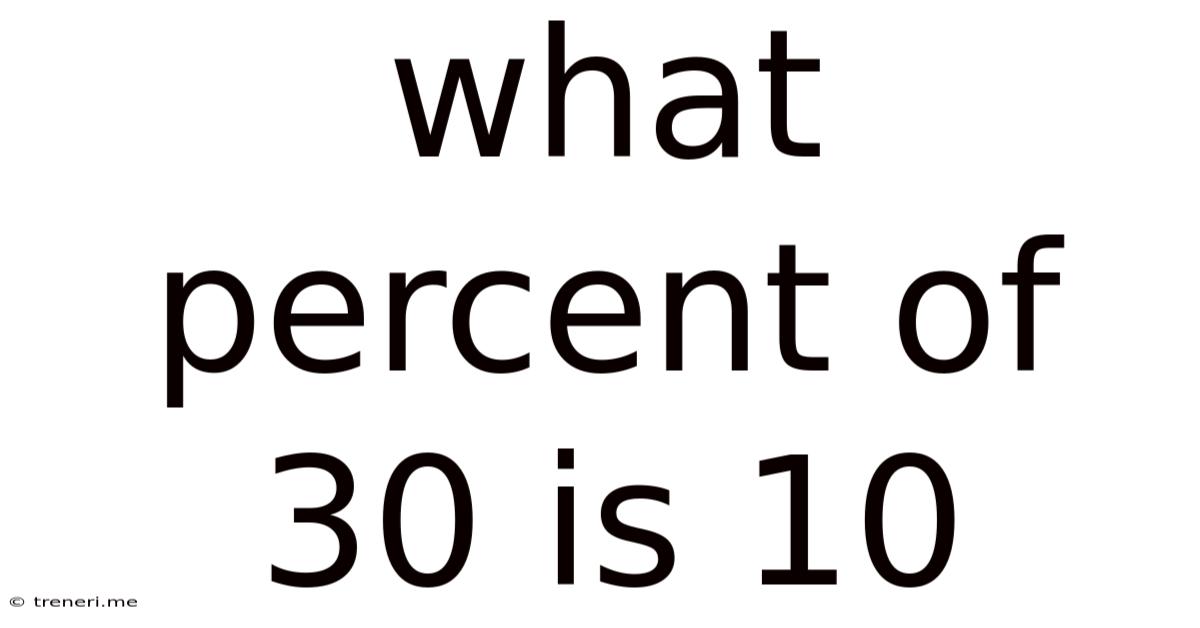
Table of Contents
What Percent of 30 is 10? A Comprehensive Guide to Percentage Calculations
Finding what percentage one number represents of another is a fundamental mathematical skill with broad applications in various fields, from finance and statistics to everyday life. This article delves deep into the question: "What percent of 30 is 10?" We will not only answer this specific question but also equip you with the knowledge and tools to tackle similar percentage problems with ease. We'll explore different methods for calculating percentages, discuss practical examples, and offer tips for improving your understanding of this crucial concept.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are used to express proportions, rates, or changes. They provide a standardized way to compare different quantities, making them incredibly useful in various contexts.
Method 1: Using the Formula
The most straightforward method to determine what percent of 30 is 10 involves using a simple percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 10 (the number we want to express as a percentage)
- Whole: 30 (the total number)
Substituting these values into the formula:
(10 / 30) * 100% = 33.33%
Therefore, 10 is 33.33% of 30.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation that states two ratios are equal. We can represent the problem as:
10/30 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
30x = 1000
x = 1000 / 30
x = 33.33
So, again, we find that 10 is 33.33% of 30.
Method 3: Using Decimal Equivalents
We can also approach this problem using decimal equivalents. First, we find the decimal representation of the fraction 10/30:
10 / 30 = 0.3333...
To convert this decimal to a percentage, we multiply by 100%:
0.3333... * 100% = 33.33%
This method offers a slightly different perspective on the calculation but leads to the same result.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in many real-world scenarios. Here are a few examples:
Finance:
- Calculating discounts: If a store offers a 20% discount on an item priced at $50, you can calculate the discount amount and the final price using percentage calculations.
- Determining interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Analyzing investment returns: Investors use percentage change to track the performance of their investments.
Statistics:
- Representing data: Percentages are commonly used in statistical analysis to represent proportions of data sets.
- Calculating probabilities: Percentages can express the likelihood of events occurring.
- Interpreting survey results: Surveys frequently present results in percentages to facilitate understanding.
Everyday Life:
- Calculating tips: Determining the appropriate tip amount in a restaurant often involves calculating a percentage of the total bill.
- Understanding sales tax: Sales tax is usually expressed as a percentage of the purchase price.
- Comparing prices: Percentages can help compare the prices of similar items from different stores.
Advanced Percentage Calculations: Beyond the Basics
While the problem "What percent of 30 is 10?" is relatively straightforward, let's explore some more complex percentage calculations to broaden your understanding.
Finding the Whole When Given a Percentage and Part:
Let's say you know that 25% of a number is 15. How do you find the whole number? You can set up a proportion:
25/100 = 15/x
Cross-multiplying and solving for x gives you x = 60. Therefore, the whole number is 60.
Finding the Part When Given a Percentage and Whole:
Imagine you need to find 15% of 80. You can simply multiply 80 by 0.15 (the decimal equivalent of 15%):
80 * 0.15 = 12
Therefore, 15% of 80 is 12.
Calculating Percentage Increase or Decrease:
Percentage change is used to express the relative difference between two values. The formula is:
((New Value - Old Value) / Old Value) * 100%
For example, if a stock price increases from $50 to $60, the percentage increase is:
((60 - 50) / 50) * 100% = 20%
Similarly, if the price decreases from $60 to $50, the percentage decrease is:
((50 - 60) / 60) * 100% = -16.67%
Tips for Mastering Percentage Calculations
- Practice Regularly: The key to mastering percentages is consistent practice. Solve various problems to build your confidence and understanding.
- Understand the Concepts: Ensure you grasp the underlying principles of percentages before tackling complex problems.
- Use Different Methods: Experiment with different calculation methods to find the approach that suits you best.
- Utilize Online Resources: Many online resources, including calculators and tutorials, can assist you in learning and practicing percentage calculations.
- Break Down Complex Problems: If faced with a challenging problem, break it down into smaller, more manageable steps.
Conclusion
Calculating percentages is a vital skill applicable across numerous domains. We've thoroughly addressed the question "What percent of 30 is 10?" using various methods and explored more advanced percentage calculations. By understanding these concepts and practicing regularly, you'll develop a strong foundation in percentage calculations, enabling you to confidently tackle percentage-related problems in your academic, professional, and personal life. Remember, consistent practice and a solid understanding of the underlying principles are the keys to success.
Latest Posts
Latest Posts
-
How Long Is 72 Business Hours
May 12, 2025
-
El 5 Por Ciento De 25
May 12, 2025
-
How Many Hours Is In Two Weeks
May 12, 2025
-
How Many Days Since January 1 2022
May 12, 2025
-
How To Calculate The Concentration Of Protein From Absorbance
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 30 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.