What Percent Of 5 Is 40
Treneri
Mar 23, 2025 · 4 min read
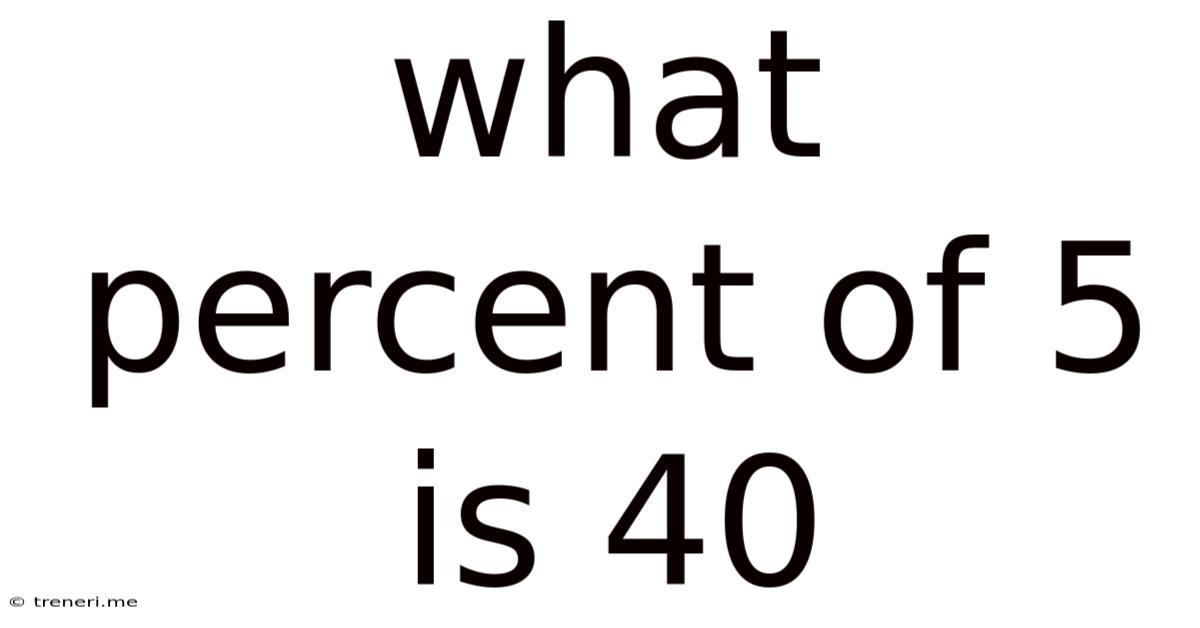
Table of Contents
What Percent of 5 is 40? Unpacking Percentages and Proportions
This seemingly simple question, "What percent of 5 is 40?", opens a door to understanding fundamental mathematical concepts like percentages, proportions, and their real-world applications. While the answer might seem counterintuitive at first glance – since 40 is much larger than 5 – the solution lies in mastering the techniques of calculating percentages and setting up proportions. This article will not only provide the answer but also delve into the underlying principles, offering various methods for solving similar problems and highlighting practical examples.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100." So, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental definition is crucial for solving percentage problems.
Method 1: Using Proportions
One of the most effective ways to solve problems involving percentages is to use proportions. A proportion is an equation stating that two ratios are equal. We can set up a proportion to represent the problem "What percent of 5 is 40?" as follows:
-
Let x represent the unknown percentage.
-
We can express the problem as a proportion: x/100 = 40/5
This proportion reads: "x out of 100 is equal to 40 out of 5." To solve for x, we cross-multiply:
-
5x = 4000
-
x = 4000 / 5
-
x = 800
Therefore, 40 is 800% of 5.
Method 2: Using the Percentage Formula
The percentage formula provides another approach to solving this problem. The formula is:
(Part / Whole) * 100% = Percentage
In our problem:
- Part = 40 (the number we're considering as a percentage of 5)
- Whole = 5 (the base number)
Substituting these values into the formula:
(40 / 5) * 100% = 800%
This confirms our previous result: 40 is 800% of 5.
Why is the Percentage Greater than 100%?
It's important to note that percentages can be greater than 100%. This simply means that the "part" is larger than the "whole." In our case, 40 is significantly larger than 5, resulting in a percentage exceeding 100%. This is perfectly valid mathematically and often encountered in real-world scenarios.
Real-World Applications of Percentages Greater than 100%
Percentages greater than 100% are commonly used in various contexts:
-
Business and Finance: A company's sales might increase by 150% compared to the previous year, indicating a substantial growth. Similarly, profits can exceed projections by a percentage greater than 100%.
-
Economics: Inflation rates can sometimes surpass 100%, signifying a dramatic increase in the general price level. Economic growth can also be expressed using percentages greater than 100%.
-
Science: In scientific experiments, measurements might exceed expectations, resulting in percentages exceeding 100%. For example, a chemical reaction might yield 120% of the predicted output.
-
Sports: A player might improve their performance by more than 100%, showcasing a significant enhancement in their skill or ability.
Further Exploration of Percentage Calculations
Let's explore more examples to solidify our understanding of percentage calculations, particularly those involving percentages greater than 100%:
Example 1: What percent of 20 is 60?
Using the proportion method: x/100 = 60/20
Cross-multiplying: 20x = 6000
Solving for x: x = 300%
Therefore, 60 is 300% of 20.
Example 2: What percent of 15 is 75?
Using the percentage formula: (75 / 15) * 100% = 500%
Therefore, 75 is 500% of 15.
Example 3: If a company's profit increased from $10,000 to $30,000, what is the percentage increase?
First, calculate the increase: $30,000 - $10,000 = $20,000
Then, use the percentage formula: ($20,000 / $10,000) * 100% = 200%
The company's profit increased by 200%.
Example 4: A student scored 80 out of 50 in an exam. What is their percentage score?
Using the percentage formula: (80 / 50) * 100% = 160%
The student scored 160%. This could indicate bonus points or extra credit in the exam.
Conclusion: Mastering Percentages for Real-World Success
Understanding percentages is a fundamental skill with widespread applications across various fields. The ability to calculate percentages, especially those exceeding 100%, is essential for interpreting data, making informed decisions, and effectively communicating quantitative information. By mastering the methods outlined in this article – using proportions and the percentage formula – you'll be well-equipped to tackle a wide range of percentage problems and confidently apply this crucial mathematical skill to your personal and professional life. Remember, practice is key to solidifying your understanding and building confidence in tackling even more complex percentage calculations. The examples provided illustrate diverse scenarios where understanding percentages beyond 100% is not only useful but crucial for accurate interpretation and analysis.
Latest Posts
Latest Posts
-
Fresh Yeast Active Dry Yeast Conversion
May 09, 2025
-
A Portion Of The Circumference Of A Circle
May 09, 2025
-
How Much Material For A Circle Skirt
May 09, 2025
-
Convert Slope Intercept Form Into Standard Form
May 09, 2025
-
How To Find The Circumference Of A Square
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 5 Is 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.