What Percent Of 7 Is 4
Treneri
May 10, 2025 · 5 min read
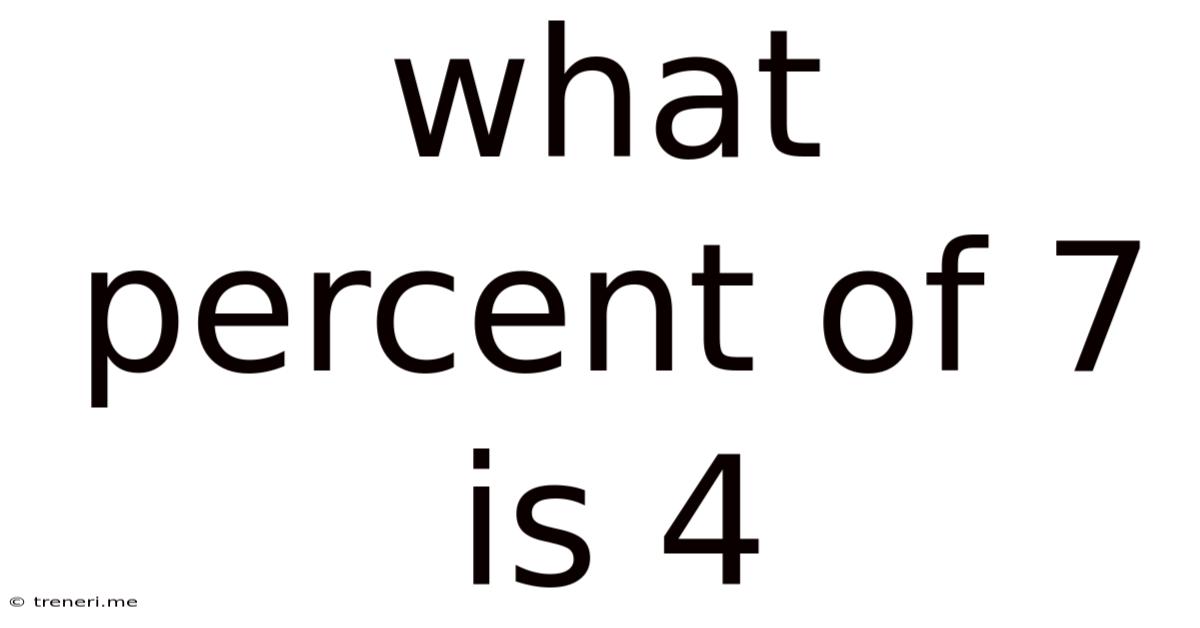
Table of Contents
What Percent of 7 is 4? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article delves into the question, "What percent of 7 is 4?" and provides a comprehensive guide to solving percentage problems, including various methods and practical applications.
Understanding the Problem: What Percent of 7 is 4?
The core of the problem lies in determining what percentage of the whole number 7 represents the value 4. We're essentially looking for a fraction (4/7) expressed as a percentage. This seemingly simple question opens doors to explore different approaches to solving percentage problems, enhancing your mathematical abilities and problem-solving skills.
Method 1: Using the Percentage Formula
The most straightforward method utilizes the basic percentage formula:
Part / Whole = Percentage / 100
In our case:
- Part: 4
- Whole: 7
- Percentage: This is what we need to find (let's represent it as 'x')
Substituting these values into the formula, we get:
4 / 7 = x / 100
To solve for 'x', we cross-multiply:
4 * 100 = 7 * x
400 = 7x
x = 400 / 7
x ≈ 57.14
Therefore, 4 is approximately 57.14% of 7.
Method 2: Converting the Fraction to a Decimal
Another approach involves converting the fraction 4/7 into a decimal and then multiplying by 100 to express it as a percentage.
- Divide the part by the whole: 4 ÷ 7 ≈ 0.5714
- Multiply the decimal by 100: 0.5714 * 100 ≈ 57.14%
This method provides the same result, reinforcing the accuracy of our calculation. The slight variation in the last decimal place might occur due to rounding during the division process.
Method 3: Using Proportions
Proportions offer another elegant way to solve percentage problems. We can set up a proportion as follows:
4/7 = x/100
Cross-multiplying yields the same equation as in Method 1:
400 = 7x
Solving for x gives us the same answer: x ≈ 57.14%
Understanding the Result and its Significance
The result, approximately 57.14%, signifies that the value 4 constitutes roughly 57.14% of the value 7. This understanding is crucial in various real-world applications. For example, if 7 represents the total number of assignments, and 4 represent the number of completed assignments, then you've completed approximately 57.14% of your work.
Practical Applications of Percentage Calculations
The ability to calculate percentages is incredibly versatile and has widespread applications in many fields:
1. Finance and Budgeting:
- Calculating interest rates: Determining the interest earned on savings or the interest paid on loans.
- Analyzing investment returns: Measuring the profitability of investments over time.
- Managing budgets: Tracking expenses, calculating percentages of income allocated to different categories.
- Understanding discounts and sales tax: Determining the final price of goods after applying discounts or adding sales tax.
2. Data Analysis and Statistics:
- Interpreting statistical data: Analyzing survey results, understanding market share, and visualizing trends.
- Calculating percentages of change: Determining the increase or decrease in values over time (e.g., population growth, economic indicators).
- Representing data graphically: Creating charts and graphs to illustrate percentage-based data effectively.
3. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants or for service providers.
- Understanding nutritional information: Interpreting the percentage of daily recommended values of nutrients in food products.
- Comparing prices: Determining which product offers better value based on discounts and unit prices.
4. Academic and Professional Settings:
- Grading and assessment: Calculating students' grades based on percentage scores.
- Performance evaluation: Measuring employee performance against targets and goals.
- Project management: Tracking progress and completion percentages of projects.
Advanced Percentage Calculations: Beyond the Basics
While the basic percentage formula is sufficient for many scenarios, some situations require more advanced techniques. These include:
1. Percentage Increase and Decrease:
Calculating the percentage increase or decrease between two numbers involves finding the difference between the two numbers, dividing it by the original number, and multiplying by 100.
For example, if a value increases from 50 to 60, the percentage increase is:
(60 - 50) / 50 * 100 = 20%
2. Calculating Percentage Change Over Time:
When dealing with multiple periods, calculating the percentage change requires considering the compounding effect. This often involves calculating percentage changes sequentially.
3. Working with Percentages of Percentages:
This involves calculating a percentage of a percentage, requiring careful attention to the order of operations. For example, finding 20% of 15% of 1000.
4. Reverse Percentage Calculations:
Sometimes, you might know the final value and the percentage change and need to calculate the original value. This often involves working backwards using algebraic manipulations of the percentage formula.
Mastering Percentages: Tips and Tricks
To enhance your proficiency in percentage calculations:
- Practice regularly: Solving diverse percentage problems regularly strengthens your understanding and speed.
- Utilize different methods: Become comfortable with various approaches to solve problems to find the method best suited to the specific situation.
- Use online calculators and tools: While understanding the underlying principles is crucial, online calculators can aid in checking your work and solving more complex problems.
- Focus on understanding the concepts: Don't just memorize formulas, focus on understanding the underlying logic and application of percentages.
- Break down complex problems: Large problems are easily manageable when broken down into smaller, more manageable steps.
Conclusion: The Power of Percentages
Understanding and calculating percentages is a critical skill applicable across numerous disciplines and daily life situations. By mastering various methods and practicing regularly, you'll gain a powerful tool for making informed decisions, analyzing data, and solving problems effectively. Remember that while the answer to "What percent of 7 is 4?" is approximately 57.14%, the true value lies in the understanding of the process and its widespread applicability. Embrace the power of percentages and watch your problem-solving abilities soar.
Latest Posts
Latest Posts
-
Cuantos Grados Celsius Son 30 Fahrenheit
May 10, 2025
-
What Is A Quarter Pound In Ounces
May 10, 2025
-
Cuanto Es 5 Pies 4 Pulgadas En Metros
May 10, 2025
-
What Is The Greatest Common Factor For 12 And 36
May 10, 2025
-
Calcium Mg Dl To Mmol L
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 7 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.