What Percent Of 8 Is 1
Treneri
May 12, 2025 · 5 min read
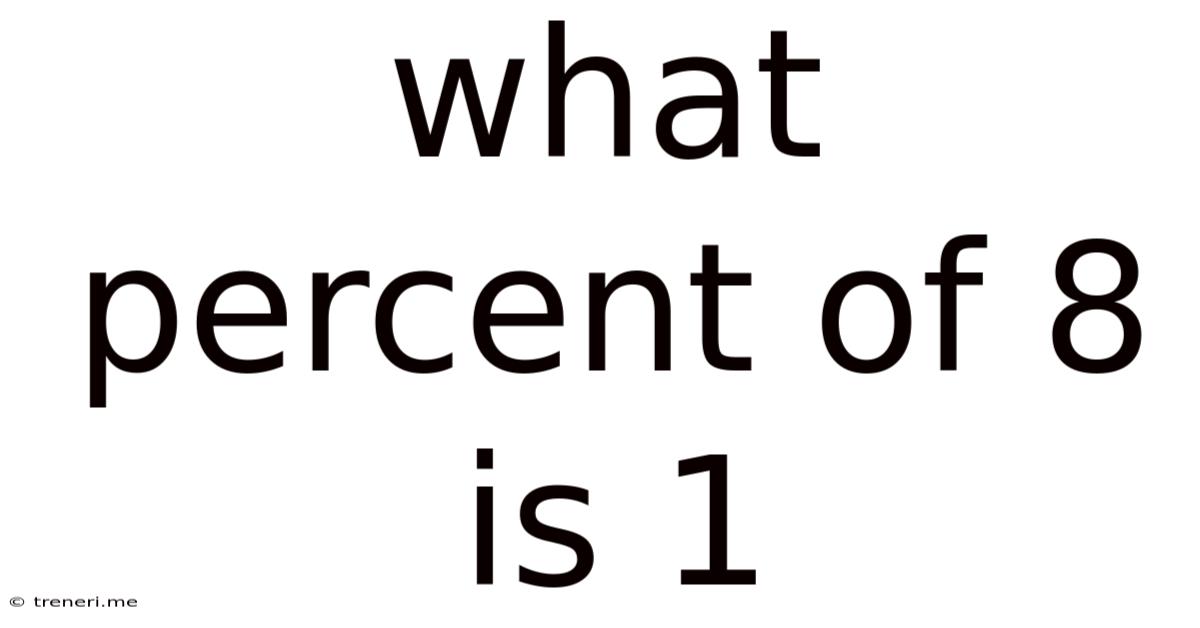
Table of Contents
What Percent of 8 is 1? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. This article will delve into the seemingly simple question: "What percent of 8 is 1?" We'll explore the solution using multiple methods, highlighting the underlying mathematical principles and providing practical applications to solidify your understanding. Furthermore, we'll address common misconceptions and expand on the broader concept of percentage calculations.
Understanding the Problem: Deconstructing "What Percent of 8 is 1?"
The question "What percent of 8 is 1?" asks us to find the percentage that, when applied to 8, results in 1. In essence, we need to determine the ratio of 1 to 8, expressed as a percentage. This involves a straightforward yet crucial understanding of percentage calculation fundamentals.
Key Concepts: Percentage, Ratio, and Proportion
Before jumping into the calculations, let's clarify some core concepts:
-
Percentage: A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
-
Ratio: A ratio compares two quantities. The ratio of 1 to 8 is written as 1:8 or 1/8.
-
Proportion: A proportion is a statement of equality between two ratios. We'll use proportions to solve our percentage problem.
Method 1: Using the Proportion Method
This method is arguably the most straightforward and widely applicable for solving percentage problems. We set up a proportion, equating the ratio of 1 to 8 with the ratio of x (our unknown percentage) to 100.
1/8 = x/100
To solve for x, we cross-multiply:
1 * 100 = 8 * x
100 = 8x
Now, divide both sides by 8:
x = 100/8
x = 12.5
Therefore, 1 is 12.5% of 8.
Method 2: Using the Decimal Method
This method involves converting the fraction 1/8 into a decimal and then multiplying by 100 to express it as a percentage.
First, divide 1 by 8:
1 ÷ 8 = 0.125
Next, multiply the decimal by 100 to convert it to a percentage:
0.125 * 100 = 12.5%
Again, we arrive at the conclusion that 1 is 12.5% of 8.
Method 3: Using the Formula Method
A more general formula for percentage problems is:
(Part / Whole) * 100% = Percentage
In our case:
Part = 1 Whole = 8
Substituting these values:
(1 / 8) * 100% = 12.5%
This formula provides a structured approach applicable to various percentage problems, offering flexibility and adaptability.
Practical Applications and Real-World Examples
The concept of finding a percentage of a number has widespread applications. Here are a few examples:
-
Calculating Discounts: If an item originally costs $8 and is discounted to $1, the discount percentage is 12.5%.
-
Determining Test Scores: If a test has 8 questions, and a student answers 1 correctly, their score is 12.5%.
-
Analyzing Financial Data: In financial analysis, understanding percentages is crucial for interpreting financial statements, calculating returns on investment, and analyzing growth rates. For instance, if a company’s profit was $1 million out of a total revenue of $8 million, then the profit margin is 12.5%.
-
Understanding Survey Results: If 1 out of 8 people surveyed preferred a particular product, the preference rate is 12.5%.
-
Scientific Research: In scientific research, calculating percentages is vital for analyzing experimental data and presenting results.
These are just a few examples illustrating the wide range of applications of percentage calculations. Mastering percentage calculations is essential for effective problem-solving and data interpretation in various aspects of life.
Common Misconceptions and Errors to Avoid
While seemingly straightforward, percentage calculations can sometimes lead to misunderstandings. Let's address some common errors:
-
Incorrect Setup of Proportions: Students often incorrectly set up the proportion, reversing the ratios. It's crucial to ensure the correct ratio is used (Part/Whole).
-
Mistakes in Decimal Conversions: Errors can occur when converting decimals to percentages and vice-versa. Remember to multiply by 100 when converting a decimal to a percentage and divide by 100 when converting a percentage to a decimal.
-
Misinterpreting the Problem: Carefully read the question to identify the part and the whole. Understanding the context is key to setting up the correct calculation.
-
Rounding Errors: Be mindful of rounding errors, especially when working with decimals. If the problem requires a certain level of precision, ensure your answer reflects that accuracy.
Expanding the Concept: Working with Different Percentages
Now that we've solved the problem, "What percent of 8 is 1?", let's expand our understanding by exploring how to find a specific percentage of a number and vice-versa.
Finding a Percentage of a Number
To find x% of a number y, we can use the formula:
(x/100) * y
For example, to find 25% of 8:
(25/100) * 8 = 2
Finding What Percent One Number is of Another
To find what percent number a is of number b, we use the formula:
(a/b) * 100%
For example, to find what percent 2 is of 8:
(2/8) * 100% = 25%
Conclusion: Mastering Percentage Calculations for Success
Understanding percentage calculations is a critical skill with far-reaching applications. This article has explored multiple methods for solving the problem, "What percent of 8 is 1?", highlighting the fundamental principles of percentages, ratios, and proportions. We've also examined practical applications, common errors, and expanded on the broader concept of percentage calculations. By grasping these concepts and practicing the methods outlined, you'll be well-equipped to tackle various percentage problems confidently and accurately. Remember to carefully read the problem statement, correctly set up your calculations, and double-check your answers for accuracy. The ability to proficiently handle percentages will enhance your analytical skills and improve your problem-solving capabilities across many aspects of your life and career.
Latest Posts
Latest Posts
-
5 Year Balloon 30 Year Amortization
May 12, 2025
-
What Does The Uv Have To Be To Get Tan
May 12, 2025
-
Cuanto Es 9 Grados En Fahrenheit
May 12, 2025
-
Work Out The Lengths Of Sides A And B
May 12, 2025
-
120 Ml Of Milk To Cups
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 8 Is 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.