What Percentage Is 24 Out Of 30
Treneri
May 12, 2025 · 5 min read
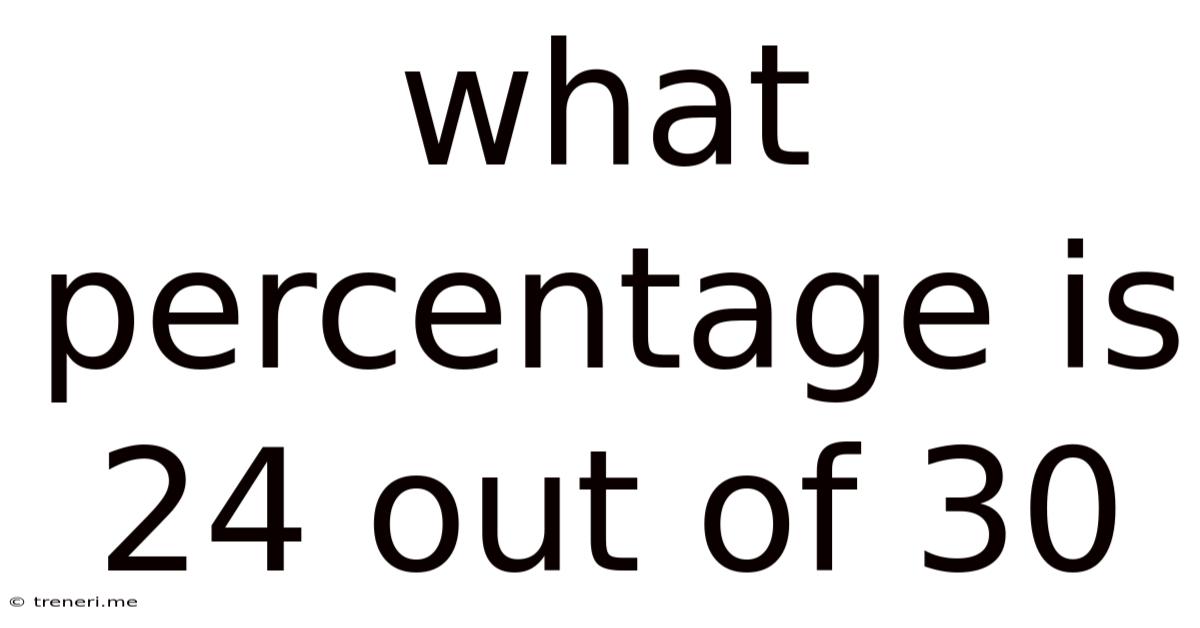
Table of Contents
What Percentage is 24 out of 30? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from academic assignments and financial management to everyday decision-making. Understanding how to determine what percentage 24 is out of 30, for instance, is not just about solving a single problem; it’s about grasping the underlying principles of percentage calculations that can be applied to numerous scenarios. This comprehensive guide will not only answer the question directly but also delve into the broader context of percentage calculations, providing you with the tools and knowledge to tackle similar problems with confidence.
Understanding Percentages: The Basics
Before we dive into calculating the specific percentage, let's solidify our understanding of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" is used to represent "percent," meaning "out of one hundred." So, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Key Terms and Concepts
- Numerator: The top number in a fraction (in our case, 24). This represents the part of the whole we are interested in.
- Denominator: The bottom number in a fraction (in our case, 30). This represents the whole amount.
- Percentage: The ratio of the numerator to the denominator, expressed as a number out of 100.
Calculating the Percentage: 24 out of 30
To determine what percentage 24 is out of 30, we can follow these steps:
-
Set up a fraction: Express the problem as a fraction: 24/30.
-
Convert the fraction to a decimal: Divide the numerator (24) by the denominator (30): 24 ÷ 30 = 0.8
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.8 x 100 = 80
Therefore, 24 out of 30 is 80%.
Alternative Methods for Percentage Calculation
While the above method is straightforward, there are other approaches you can use, depending on your preference and the complexity of the problem:
Method 2: Using Proportions
You can solve this using proportions. We know that the percentage we're looking for (let's call it 'x') is related to the whole (30) in the same way that 24 is related to 100. We can set up a proportion:
24/30 = x/100
To solve for x, cross-multiply:
30x = 2400
x = 2400/30
x = 80
Therefore, x = 80%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function. You can simply enter 24 ÷ 30 and then multiply by 100 to obtain the percentage directly. This method is particularly useful for more complex percentage calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in various real-world scenarios:
1. Academic Performance:
Calculating grades, understanding class rankings, and assessing progress in different subjects all rely heavily on percentage calculations. For example, if you scored 24 out of 30 on a test, knowing it's 80% helps you understand your performance relative to the total possible score.
2. Financial Management:
Percentages are fundamental to understanding interest rates, discounts, taxes, tips, and investment returns. For example, calculating the interest on a loan or the discount on a sale price requires accurate percentage calculations. Determining your savings rate or investment growth also depends on percentages.
3. Business and Economics:
In business, percentages are used extensively for profit margins, market share analysis, growth rates, and sales figures. Analyzing market trends, assessing the success of marketing campaigns, and projecting future revenue all rely on percentage calculations. Understanding profit margins (percentage of profit relative to cost), and sales growth (percentage increase in sales over a given period) are vital for business decision-making.
4. Data Analysis and Statistics:
Percentages are frequently used to present data in a clear and concise manner. They allow for easy comparison of different data sets and aid in identifying trends and patterns. For example, when analyzing survey results or demographic data, percentages provide a meaningful way to represent proportions within the population being studied.
5. Everyday Life:
Even in everyday situations, percentages are prevalent. From calculating sales tax to determining the tip at a restaurant, understanding percentages makes daily financial transactions easier to manage. Understanding percentage discounts helps in making informed purchasing decisions, leading to better financial planning.
Beyond the Basics: More Complex Percentage Problems
While calculating 24 out of 30 is a relatively simple problem, mastering percentage calculations involves understanding more complex scenarios:
Calculating Percentage Increase or Decrease:
These calculations involve finding the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] x 100
For example, if a product's price increased from $20 to $25, the percentage increase is:
[(25 - 20) / 20] x 100 = 25%
Finding the Original Value:
Sometimes, you know the percentage and the resulting value, but need to find the original value. This requires working backward using algebraic methods.
For example, if a price after a 20% discount is $80, the original price can be calculated as:
Original Price x (1 - 0.20) = $80
Original Price x 0.80 = $80
Original Price = $80 / 0.80 = $100
Dealing with Multiple Percentages:
Calculating percentages involving multiple increases or decreases requires careful consideration of the order of operations. For instance, a 10% increase followed by a 10% decrease does not result in the original value; it will result in a slightly lower value because the second percentage is calculated on a larger base.
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations takes practice. Here are some tips to improve your skills:
- Practice regularly: Work through various problems, starting with simple ones and gradually increasing the complexity.
- Use different methods: Try solving the same problem using different methods (fraction, proportion, calculator) to deepen your understanding.
- Visualize the problem: Imagine the problem visually as a pie chart or bar graph to better understand the relationship between the parts and the whole.
- Check your work: Always double-check your calculations to ensure accuracy. Use estimation to verify your answers are in the right ballpark.
- Seek help when needed: Don't hesitate to seek assistance from teachers, tutors, or online resources if you encounter difficulties.
By understanding the fundamental principles of percentage calculations and practicing regularly, you'll be able to confidently tackle a wide range of percentage problems, from simple calculations like determining what percentage 24 is out of 30 to more complex scenarios encountered in various aspects of your life. The ability to effectively utilize percentage calculations is an invaluable skill that enhances your problem-solving abilities and decision-making processes in diverse contexts.
Latest Posts
Latest Posts
-
Cuanto Es 7 5 Ft En Centimetros
May 13, 2025
-
How To Find Class Width Of A Histogram
May 13, 2025
-
Calculate Heat Capacity Of A Calorimeter
May 13, 2025
-
How Many Miles Is 450 Kilometers
May 13, 2025
-
Highest Common Factor Of 72 And 96
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 24 Out Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.