What Percentage Is 50 Of 1000
Treneri
May 13, 2025 · 5 min read
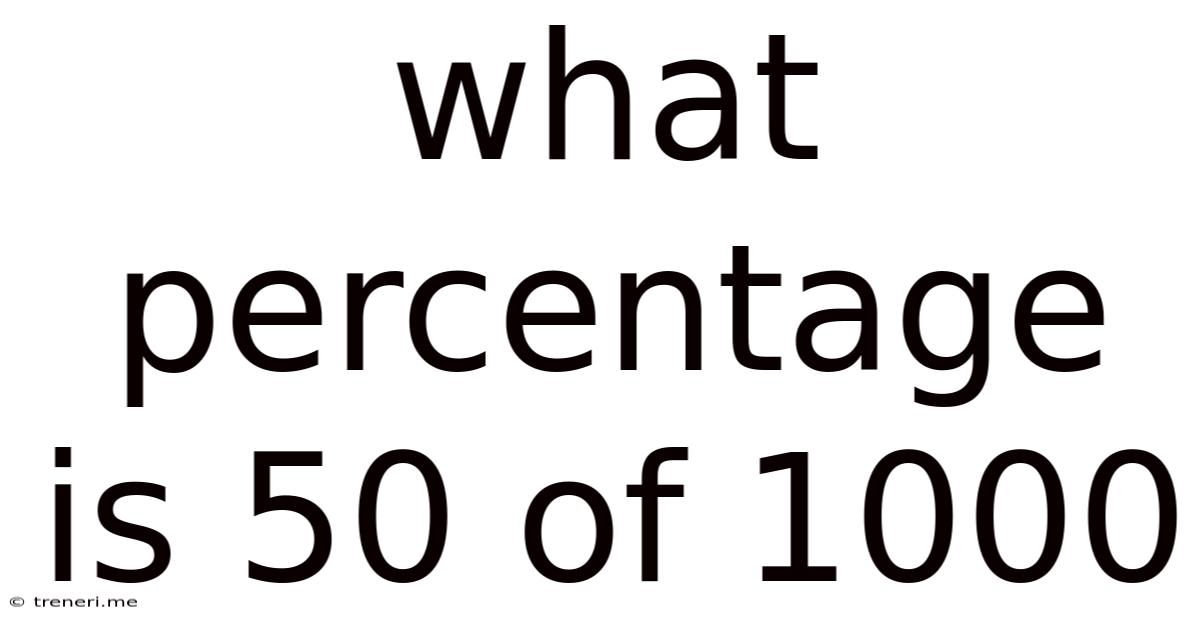
Table of Contents
What Percentage is 50 of 1000? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and tax rates to comprehending statistical data and financial reports. This comprehensive guide will delve into the question, "What percentage is 50 of 1000?", providing not only the answer but also a detailed explanation of the underlying principles and various methods for calculating percentages. We'll explore different approaches, suitable for various skill levels, ensuring a thorough understanding of percentage calculations. By the end, you'll be equipped to confidently tackle any percentage problem you encounter.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal.
Key Terminology
- Percentage: The number expressed as a fraction of 100 (e.g., 50%).
- Part: The number that represents a portion of the whole (e.g., 50 in this case).
- Whole: The total number or quantity (e.g., 1000 in this case).
Calculating "What Percentage is 50 of 1000?"
There are several ways to calculate what percentage 50 represents of 1000. Let's explore the most common methods:
Method 1: Using the Formula
The most straightforward method utilizes the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
(50 / 1000) x 100% = 5%
Therefore, 50 is 5% of 1000.
Method 2: Simplifying the Fraction
We can simplify the fraction 50/1000 before multiplying by 100%. Both 50 and 1000 are divisible by 50:
50/1000 = 1/20
Now, convert the fraction 1/20 to a percentage:
(1/20) x 100% = 5%
This method demonstrates that simplifying the fraction can make the calculation easier.
Method 3: Using Proportions
We can also solve this using proportions:
50/1000 = x/100
Where 'x' represents the percentage we are trying to find. To solve for x, we cross-multiply:
1000x = 5000
x = 5000/1000
x = 5
Therefore, x = 5%, confirming our previous results. This method is particularly useful when dealing with more complex percentage problems.
Beyond the Basic Calculation: Expanding Your Understanding
While we've answered the primary question, let's delve deeper into the broader implications of percentage calculations and explore related scenarios.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various real-world situations. Here are some examples:
1. Sales and Discounts
Retailers frequently advertise discounts as percentages. For instance, a "20% off" sale means you'll pay 80% of the original price. Understanding percentage calculations allows you to quickly determine the final price after a discount.
2. Taxes and Interest Rates
Taxes are often expressed as percentages of income or purchase price. Similarly, interest rates on loans and investments are typically stated as annual percentages. A clear understanding of percentages is crucial for managing personal finances and making informed decisions about borrowing and investing.
3. Statistical Analysis
Percentages are widely used in statistical data representation. For example, survey results, election polls, and market research often present data in terms of percentages to facilitate easy comprehension and comparison.
4. Financial Reporting
Financial statements, such as balance sheets and income statements, utilize percentages extensively to illustrate key ratios and trends. Understanding percentage calculations is fundamental to interpreting these statements and assessing the financial health of a company.
5. Scientific and Engineering Applications
Percentages play a role in various scientific and engineering fields. For example, calculating efficiency, error margins, and concentrations often involves percentage calculations.
Advanced Percentage Calculations: Going Further
While the calculation of "What percentage is 50 of 1000?" is relatively straightforward, let's consider some more complex scenarios:
1. Calculating Percentage Increase or Decrease
This involves determining the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] x 100%
For example, if a product's price increased from $100 to $120, the percentage increase is:
[(120 - 100) / 100] x 100% = 20%
2. Finding the Original Value after a Percentage Change
Suppose you know the final value after a percentage increase or decrease, and you want to find the original value. You can use the following formula:
Original Value = Final Value / (1 + Percentage Change/100) (for increase)
Original Value = Final Value / (1 - Percentage Change/100) (for decrease)
For example, if a product costs $120 after a 20% increase, the original price was:
Original Value = 120 / (1 + 20/100) = $100
3. Calculating Percentage of a Percentage
This involves finding a percentage of another percentage. For instance, finding 10% of 25% would be:
(10/100) x (25/100) x 100% = 2.5%
Tips and Tricks for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Use a calculator: For more complex calculations, a calculator can save time and increase accuracy.
- Break down complex problems: Divide complex problems into smaller, manageable steps.
- Understand the context: Always consider the context of the problem to ensure you're using the correct formula and interpretation.
- Check your work: Always double-check your calculations to avoid errors.
Conclusion
Understanding percentage calculations is a crucial life skill. We’ve addressed the question, "What percentage is 50 of 1000?", demonstrating various methods to arrive at the correct answer: 5%. Beyond this basic calculation, we've explored numerous real-world applications and more complex percentage scenarios. By mastering these concepts and practicing regularly, you’ll build confidence and proficiency in handling any percentage-related problem you encounter. Remember to practice regularly and utilize the various methods to solidify your understanding. The more you work with percentages, the more intuitive they will become.
Latest Posts
Latest Posts
-
7 Out Of 24 As A Percentage
May 14, 2025
-
How To Determine Concentration From Absorbance
May 14, 2025
-
How Long Is 72 Weeks In Months
May 14, 2025
-
Average Toilet Paper Usage Per Person Per Week
May 14, 2025
-
Cuanto Falta Para El 29 De Marzo 2024
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 50 Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.