What Percentage Is 60 Out Of 70
Treneri
May 10, 2025 · 5 min read
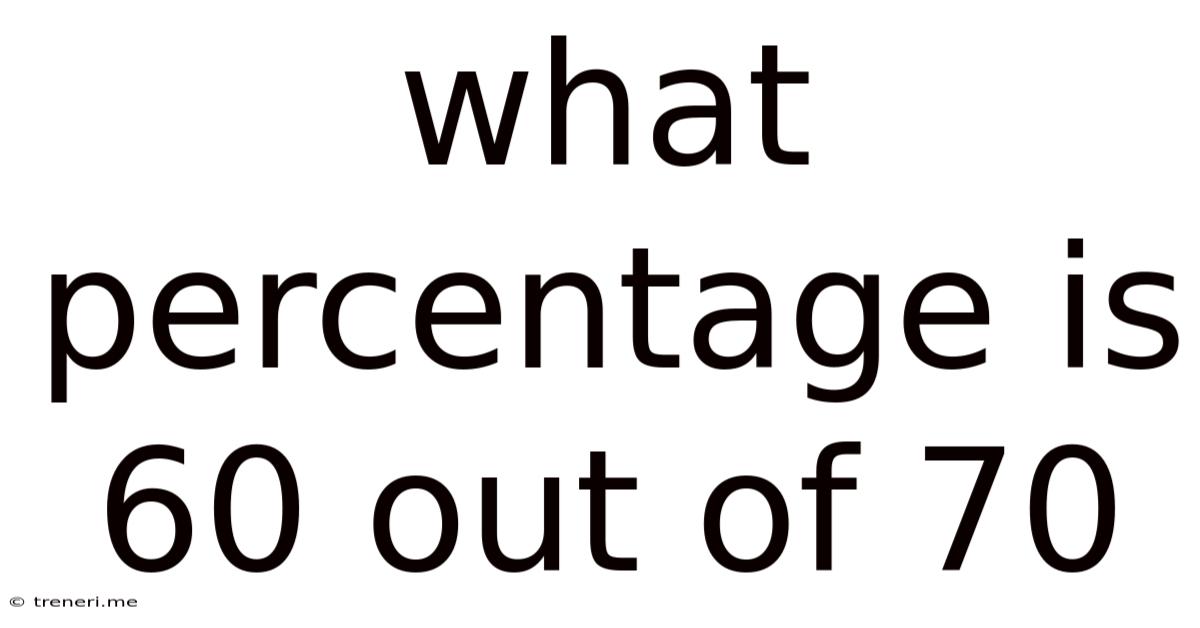
Table of Contents
What Percentage is 60 Out of 70? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from academic pursuits to professional finance. Understanding how to determine what percentage one number represents of another is crucial for interpreting data, making comparisons, and solving various real-world problems. This comprehensive guide will delve into calculating the percentage that 60 represents out of 70, providing a step-by-step process, exploring different calculation methods, and offering practical applications.
Understanding Percentages
Before diving into the specific calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to represent "percent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Calculating the Percentage: 60 out of 70
To determine what percentage 60 is of 70, we'll use a straightforward formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 60 (the number we want to express as a percentage)
- Whole: 70 (the total number)
Substituting these values into the formula:
(60 / 70) * 100% = Percentage
This simplifies to:
0.857142857 * 100% ≈ 85.71%
Therefore, 60 is approximately 85.71% of 70.
Alternative Calculation Methods
While the above method is the most common and straightforward, there are alternative approaches to arrive at the same answer.
Method 2: Using Decimal Conversion
- Divide the part by the whole: 60 / 70 = 0.857142857
- Multiply the decimal by 100: 0.857142857 * 100 = 85.7142857
- Add the percentage symbol: 85.7142857%
This method essentially performs the same calculation as the primary method but breaks it down into two distinct steps.
Method 3: Proportion Method
This method involves setting up a proportion:
60/70 = x/100
To solve for x (the percentage), we cross-multiply:
70x = 6000
x = 6000 / 70
x ≈ 85.71
This method demonstrates the underlying relationship between ratios and percentages.
Practical Applications: Where Percentage Calculations Matter
Understanding percentage calculations is critical in numerous real-world scenarios. Here are just a few examples:
1. Academic Performance:
Imagine a student scores 60 out of 70 on a test. Calculating the percentage (85.71%) helps assess their performance relative to the total possible marks. This allows for a standardized comparison across different tests and subjects. Understanding percentage grades is vital for tracking academic progress and identifying areas for improvement. Furthermore, colleges and universities often use percentage grades in determining scholarship eligibility and overall academic standing.
2. Financial Calculations:
Percentages are ubiquitous in finance. Calculating interest rates, discounts, tax rates, profit margins, and investment returns all rely on percentage calculations. For example, if a retailer offers a 20% discount on an item, calculating the final price requires understanding percentages. Similarly, calculating the amount of tax payable on an income necessitates proficiency in percentage calculations. These skills are critical for personal finance management and investment decision-making.
3. Data Analysis and Interpretation:
Across various fields, data analysis often involves interpreting data presented as percentages. For example, understanding the percentage of market share held by a particular company, the percentage of respondents who favor a specific product in a survey, or the percentage change in stock prices over time requires a solid grasp of percentage calculations. This skill is essential for drawing meaningful conclusions from data and making informed decisions. The ability to quickly calculate and interpret percentages enhances efficiency and understanding within data analysis processes.
4. Business and Sales:
In business, percentage calculations are crucial for evaluating sales performance, profit margins, conversion rates, customer satisfaction, and growth trends. Tracking the percentage increase or decrease in sales revenue over time provides insights into business performance. Analyzing the conversion rate (the percentage of website visitors who make a purchase) helps optimize marketing strategies. Monitoring customer satisfaction through feedback surveys allows businesses to track their percentage of satisfied clients. Understanding these percentages is key to informed decision-making and business strategy.
5. Scientific Research:
In many scientific fields, experimental data is often represented as percentages. For example, calculating the percentage of participants who respond positively to a treatment in a clinical trial, or the percentage of a particular substance found in a sample, is critical for analysis and conclusions. Accuracy and precision in calculating percentages are vital for drawing valid scientific inferences.
Rounding and Precision
It's important to note that the percentage we calculated (85.71%) is a rounded value. The exact decimal value is 85.7142857..., which continues indefinitely. The level of precision required depends on the context. In some cases, rounding to the nearest whole number (86%) may suffice, while in others, greater accuracy might be necessary, such as using two or three decimal places (85.71% or 85.714%). Always consider the context and the level of accuracy required when rounding percentage values.
Common Mistakes to Avoid
While calculating percentages is relatively straightforward, there are some common mistakes to watch out for:
- Incorrect Formula: Using an incorrect formula is a fundamental error that leads to inaccurate results. Ensure you use the correct formula: (Part / Whole) * 100%.
- Order of Operations: Remembering the order of operations (PEMDAS/BODMAS) is important. Division should be performed before multiplication.
- Rounding Errors: Rounding too early in the calculation can lead to significant inaccuracies. It's better to round only at the very end.
- Unit Confusion: Ensuring the units are consistent throughout the calculation is essential. Using inconsistent units can lead to significant errors.
Conclusion
Calculating percentages is a fundamental skill with wide-ranging applications. Understanding the methods outlined in this guide, from the basic formula to alternative approaches, empowers you to tackle percentage calculations confidently and accurately. By mastering these calculations, you'll be better equipped to interpret data, make informed decisions, and solve real-world problems across various disciplines. Remember to always consider the context, level of precision needed, and potential sources of error to ensure accurate and meaningful results. Practice is key to building proficiency, so tackle various percentage problems to hone your skills and build confidence in your calculations.
Latest Posts
Latest Posts
-
19 Oz Equals How Many Cups
May 11, 2025
-
Cuantas Son 12 Onzas En Mililitros
May 11, 2025
-
Moment Of Inertia For I Beam Calculator
May 11, 2025
-
Can You Tan With Uv 6
May 11, 2025
-
2 1 To The Power Of 2
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 60 Out Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.