What Percentage Of 11 Is 4
Treneri
May 10, 2025 · 5 min read
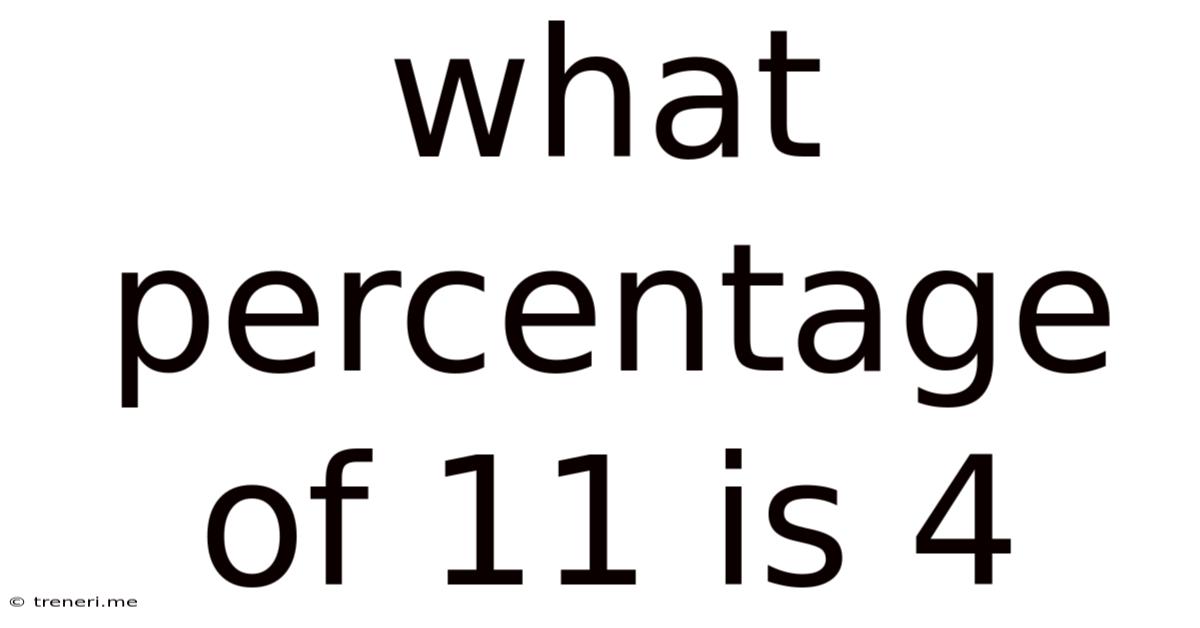
Table of Contents
What Percentage of 11 is 4? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percentage of 11 is 4?", opens the door to a fascinating exploration of percentage calculations and their real-world applications. While the answer itself is straightforward, understanding the underlying principles and methods allows you to tackle more complex percentage problems with confidence. This article will not only provide the solution but also delve into various approaches, explaining the concepts behind percentage calculations and offering practical examples.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's establish a firm grasp of what percentages represent. A percentage is simply a fraction expressed as a number out of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10% means 10 out of 100, or 10/100, which simplifies to 1/10.
This understanding is crucial because percentages allow us to compare proportions across different quantities. Instead of working with fractions or decimals, percentages provide a standardized and easily understandable way to represent parts of a whole.
Method 1: Using Proportions
One of the most intuitive methods for solving percentage problems involves setting up a proportion. A proportion is simply an equation stating that two ratios are equal. In our case, we can set up the following proportion:
4/11 = x/100
Where:
- 4 represents the part.
- 11 represents the whole.
- x represents the unknown percentage we're trying to find.
- 100 represents the total percentage (100%).
To solve for x, we can cross-multiply:
11x = 4 * 100
11x = 400
x = 400/11
x ≈ 36.36
Therefore, 4 is approximately 36.36% of 11.
Method 2: Using Decimal Conversion
Another effective approach involves converting the fraction into a decimal and then multiplying by 100 to obtain the percentage. Let's follow this method step-by-step:
-
Form the fraction: We begin by forming the fraction 4/11, representing the part (4) over the whole (11).
-
Convert to decimal: Divide 4 by 11 using a calculator or long division. This yields approximately 0.3636.
-
Multiply by 100: Multiply the decimal (0.3636) by 100 to convert it into a percentage. This gives us approximately 36.36%.
Thus, we arrive at the same result as before: 4 is approximately 36.36% of 11.
Method 3: Using the Percentage Formula
The standard percentage formula is:
(Part / Whole) * 100 = Percentage
Applying this formula to our problem:
(4 / 11) * 100 ≈ 36.36%
This method directly reflects the core concept of percentages: finding the ratio of the part to the whole and then scaling it up to a value out of 100. This formula is highly versatile and can be used to solve a wide array of percentage problems.
Understanding the Approximation
It's crucial to note that the answer we obtained (36.36%) is an approximation. The decimal 0.363636... is a repeating decimal, meaning it goes on infinitely. We've rounded the answer to two decimal places for practical purposes. The degree of precision required will depend on the context of the problem. In some situations, rounding to the nearest whole number (36%) might suffice, while in others, more decimal places might be necessary.
Real-World Applications: Percentage Calculations in Everyday Life
Understanding percentage calculations isn't just an academic exercise; it's a crucial skill for navigating everyday life. Here are a few examples:
-
Calculating discounts: When shopping, you'll frequently encounter sales offering a certain percentage off. Understanding percentages helps you quickly determine the final price after the discount is applied. For example, a 20% discount on a $50 item means you'll save $10 (20% of $50) and pay $40.
-
Analyzing financial data: Percentages are fundamental to understanding financial statements, calculating interest rates, and tracking investment returns. For example, if your investment grows by 10% in a year, you'll need to understand percentage calculations to determine the actual increase in value.
-
Understanding statistics: Percentages are extensively used in statistics to represent proportions, probabilities, and trends. News reports, scientific studies, and surveys frequently utilize percentages to communicate data effectively.
-
Calculating tax rates: Sales tax, income tax, and other taxes are often expressed as percentages. You need to understand percentage calculations to determine the total cost of an item including tax or the amount of tax you owe.
-
Determining grades and scores: In educational settings, grades and scores are often expressed as percentages. Understanding percentages helps you evaluate your performance and track your progress.
Beyond the Basics: More Complex Percentage Problems
While the "what percentage of 11 is 4" problem is relatively simple, the principles discussed here extend to more complex scenarios. You might encounter problems involving:
-
Finding the whole when the percentage and part are known. For instance, "If 25% of a number is 10, what is the number?"
-
Calculating percentage increase or decrease. This involves comparing two values and expressing the change as a percentage.
-
Working with compound percentages. Compound percentages involve applying a percentage to a value multiple times, often over a period of time (such as compound interest calculations).
Mastering the fundamentals of percentage calculations, as illustrated by the simple problem of determining what percentage of 11 is 4, provides a solid foundation for tackling more intricate percentage problems. By understanding the different methods and their underlying principles, you equip yourself with a valuable skill applicable across numerous real-world scenarios. The ability to quickly and accurately calculate percentages empowers you to make informed decisions, analyze data, and navigate various aspects of daily life with greater confidence.
Latest Posts
Latest Posts
-
Cuanto Es 4 5 Pies En Centimetros
May 11, 2025
-
0 75 Cu Ft To Lbs Soil
May 11, 2025
-
Find The Perimeter Of The Rectangle In Yards
May 11, 2025
-
What Is The Greatest Common Factor Of 4 And 7
May 11, 2025
-
How Many Miles Is 1 7 Km
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 11 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.