What Percentage Of 20 Is 3
Treneri
May 14, 2025 · 5 min read
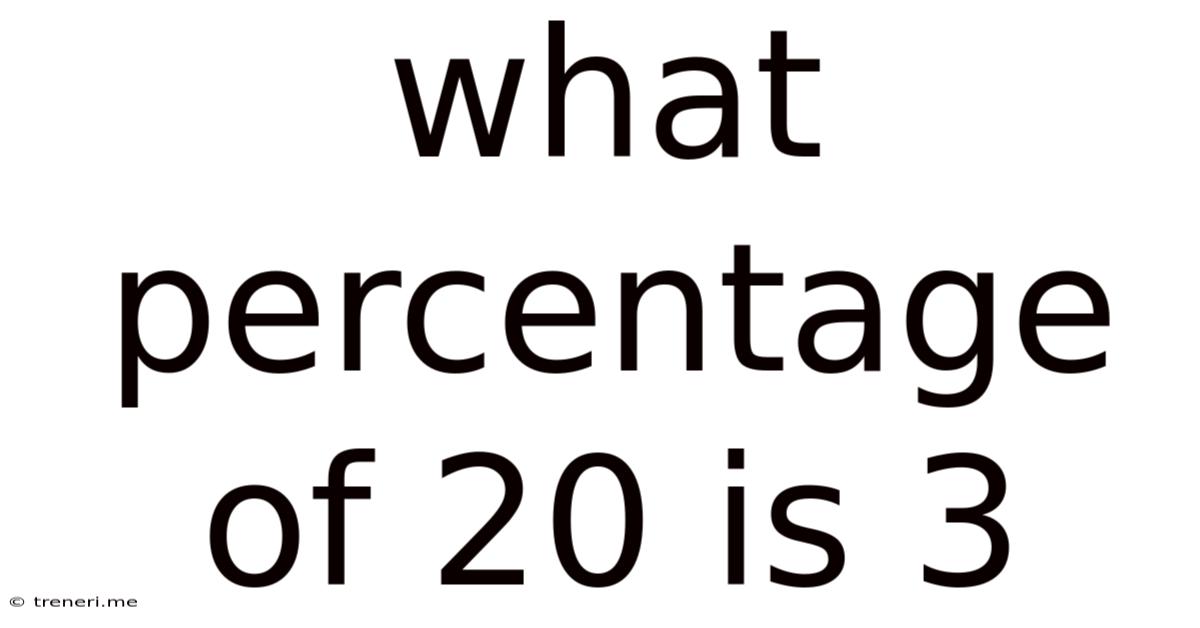
Table of Contents
What Percentage of 20 is 3? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percentage of 20 is 3?", opens the door to a fascinating exploration of percentage calculations, their real-world applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the how and why behind the calculation is crucial for anyone looking to master percentages and apply them effectively in various contexts.
Understanding Percentages: The Foundation
Before we dive into the specifics of this problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Percentages are used extensively in everyday life, from calculating discounts and taxes to understanding financial statements and expressing statistical data. Mastering percentage calculations is a valuable skill applicable across numerous fields.
Calculating "What Percentage of 20 is 3?"
Now, let's tackle the core question: What percentage of 20 is 3? We can solve this using a simple formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 3 (the number we're interested in finding the percentage of)
- Whole: 20 (the total number)
Substituting these values into the formula:
(3 / 20) * 100 = 15
Therefore, 3 is 15% of 20.
Different Approaches to Solving Percentage Problems
While the formula above provides a direct solution, understanding alternative approaches can deepen your comprehension of percentage calculations. Let's explore a few:
1. Using Proportions:
Percentages can be represented as proportions. We can set up a proportion:
3/20 = x/100
Where 'x' represents the percentage we're trying to find. Solving for 'x' involves cross-multiplication:
20x = 300
x = 300 / 20
x = 15
This confirms that 3 is 15% of 20.
2. Using Decimals:
Converting the fraction to a decimal can also be helpful. 3/20 = 0.15. To express this as a percentage, we simply multiply by 100:
0.15 * 100 = 15%
This method highlights the direct relationship between decimals and percentages.
Real-World Applications of Percentage Calculations
Understanding percentage calculations isn't just about solving math problems; it has significant practical applications in various real-world scenarios. Here are some examples:
-
Discounts and Sales: Retail stores frequently advertise discounts as percentages. For instance, a 20% discount on a $50 item means you'll save 20% of $50, which is $10. Understanding percentage calculations is crucial to determining the final price after a discount.
-
Taxes and Interest: Taxes and interest are often expressed as percentages. Knowing how to calculate these percentages allows you to accurately determine the total cost of an item after tax or the interest accrued on a loan or savings account.
-
Financial Analysis: Percentage calculations are fundamental in financial analysis, where metrics like profit margins, return on investment (ROI), and growth rates are expressed as percentages. These percentages help investors and businesses make informed decisions.
-
Statistical Data Analysis: Percentages are used to represent proportions in various statistical analyses. For example, survey results are often presented as percentages to show the distribution of responses. Understanding percentages is crucial for interpreting and understanding these types of data.
-
Grade Calculations: In education, your final grade is often calculated as a percentage of your total points earned. Understanding how percentages are calculated helps students understand their academic performance.
Beyond the Basics: Advanced Percentage Problems
While the problem "What percentage of 20 is 3?" provides a basic understanding of percentage calculations, more complex scenarios involve multiple steps and variables. Let's look at some examples:
Scenario 1: Finding the Whole when given the Part and Percentage
Suppose you know that 15% of a certain number is 6. How do you find that number?
We can use the formula:
(Percentage/100) * Whole = Part
Substituting the known values:
(15/100) * x = 6
Solving for x:
x = (6 * 100) / 15
x = 40
Therefore, the whole number is 40.
Scenario 2: Finding the Percentage Increase or Decrease
Imagine a stock price increased from $20 to $25. What's the percentage increase?
- Calculate the difference: $25 - $20 = $5
- Divide the difference by the original value: $5 / $20 = 0.25
- Multiply by 100 to express as a percentage: 0.25 * 100 = 25%
The stock price increased by 25%.
These examples showcase the versatility of percentage calculations and their adaptability to diverse problem types.
Tips and Tricks for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering any mathematical concept is consistent practice. Work through various percentage problems to reinforce your understanding.
-
Visual Aids: Using visual aids like diagrams or charts can help you visualize the relationship between the parts and the whole.
-
Utilize Online Calculators (for verification): While it's crucial to understand the manual calculations, online percentage calculators can be useful for verifying your answers and gaining confidence in your skills. Remember to use them as a tool for checking, not a replacement for learning the process.
-
Break Down Complex Problems: When facing complex percentage problems, break them down into smaller, manageable steps. This approach makes the problem less daunting and simplifies the solution process.
Conclusion: The Power of Percentage Understanding
The seemingly simple question, "What percentage of 20 is 3?", provides a gateway to understanding the power and versatility of percentage calculations. From everyday transactions to complex financial analyses, mastering percentages is a valuable skill that enhances decision-making and problem-solving abilities across various fields. By understanding the underlying principles and practicing regularly, you can confidently tackle any percentage-related challenge and unlock its practical applications in your life. Remember to utilize different approaches and always double-check your work to ensure accuracy. The ability to calculate and interpret percentages is a fundamental skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
24 Inches By 24 Inches In Square Feet
May 14, 2025
-
1 2 Cubic Yard To Square Feet
May 14, 2025
-
How Many Years Is 125 Months
May 14, 2025
-
Subtract The Quotient Of 70 Divided By 2 From 60
May 14, 2025
-
How Much Hours Is 100 Days
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 20 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.