What Percentage Of 30 Is 27
Treneri
May 14, 2025 · 4 min read
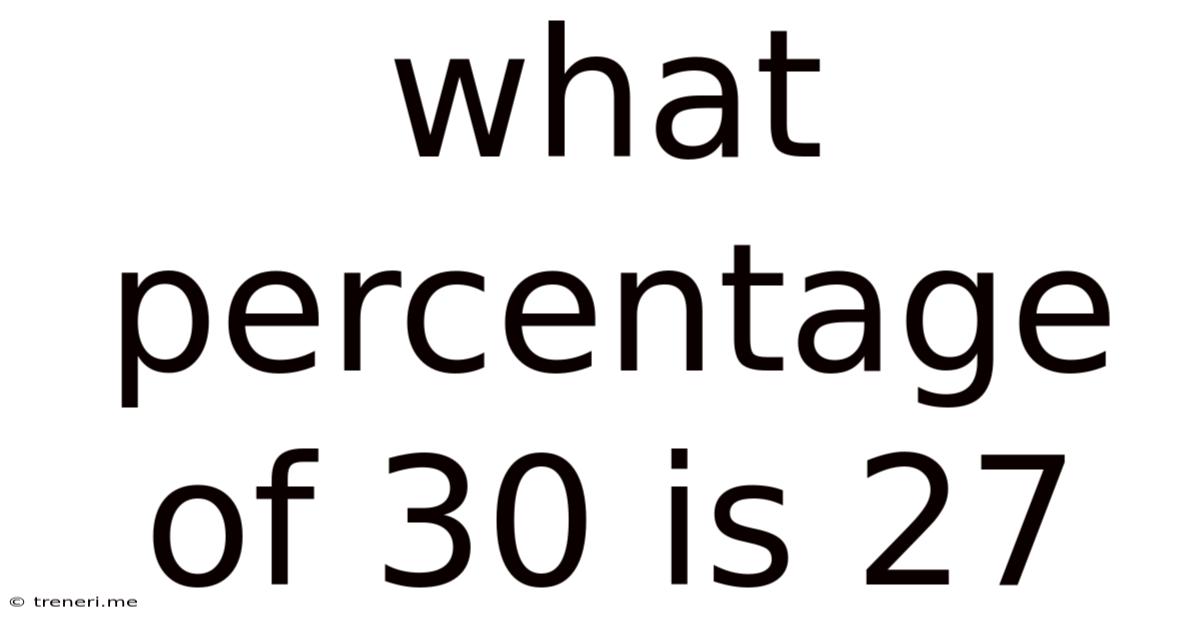
Table of Contents
What Percentage of 30 is 27? A Comprehensive Guide to Percentage Calculations
Finding what percentage one number represents of another is a fundamental skill in mathematics with widespread applications in various fields, from finance and business to everyday life. This comprehensive guide will not only answer the question, "What percentage of 30 is 27?" but also delve into the underlying principles of percentage calculations, offering practical examples and techniques to master this essential concept.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this foundational concept is crucial for tackling percentage problems.
Calculating Percentages: The Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
Where:
- Part: This is the number you want to express as a percentage of the whole.
- Whole: This is the total number that the part is a fraction of.
- Percentage: This is the result, expressed as a percentage.
Solving "What Percentage of 30 is 27?"
Now, let's apply this formula to answer our specific question: "What percentage of 30 is 27?"
In this case:
- Part = 27
- Whole = 30
Substituting these values into the formula:
(27 / 30) * 100% = Percentage
This simplifies to:
0.9 * 100% = 90%
Therefore, 27 is 90% of 30.
Alternative Methods for Percentage Calculation
While the formula above is the most straightforward approach, several other methods can be used to calculate percentages, particularly useful for mental calculations or when dealing with simpler numbers:
Method 1: Using Fractions
Convert the problem into a fraction: 27/30. Then, simplify the fraction to its lowest terms: 9/10. Finally, convert the fraction to a percentage by multiplying by 100%: (9/10) * 100% = 90%.
Method 2: Using Proportions
Set up a proportion: x/100 = 27/30. Cross-multiply to solve for x: 30x = 2700. Divide both sides by 30 to find x: x = 90. Therefore, x = 90%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous everyday situations:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations. For example, calculating the interest earned on a savings account or determining the discount on a sale item requires a firm grasp of percentages.
-
Business: Businesses use percentages to analyze sales data, track market share, and project future growth. Understanding profit margins, return on investment (ROI), and various financial ratios all involve percentage calculations.
-
Science: Percentages are frequently used to represent experimental data, statistical results, and variations in measurements. For example, the concentration of a solution is often expressed as a percentage.
-
Everyday Life: Calculating tips at restaurants, understanding sales discounts, figuring out the percentage of a completed task, or determining the nutritional content of food all involve percentage calculations.
Advanced Percentage Calculations: Finding the Whole or the Part
The basic percentage formula can be rearranged to solve for the whole or the part if you know the percentage and one of the other values:
-
Finding the Whole: If you know the percentage and the part, you can rearrange the formula to solve for the whole: Whole = (Part / Percentage) * 100
-
Finding the Part: If you know the percentage and the whole, you can rearrange the formula to solve for the part: Part = (Percentage / 100) * Whole
Let's illustrate with examples:
Example 1: Finding the Whole
If 20% of a number is 10, what is the number?
Using the rearranged formula: Whole = (10 / 20) * 100 = 50
Example 2: Finding the Part
What is 35% of 80?
Using the rearranged formula: Part = (35 / 100) * 80 = 28
Percentage Increase and Decrease
Calculating percentage increases and decreases are also common tasks. The formulas are:
-
Percentage Increase: [(New Value - Old Value) / Old Value] * 100%
-
Percentage Decrease: [(Old Value - New Value) / Old Value] * 100%
For example, if a price increases from $100 to $120, the percentage increase is [(120 - 100) / 100] * 100% = 20%.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: Consistent practice is key to mastering percentage calculations. Start with simple problems and gradually increase the complexity.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles of percentages. This will allow you to apply the concepts to various scenarios.
-
Use Online Calculators and Resources: While understanding the methods is crucial, online calculators can be helpful for checking your answers and practicing with different problems.
-
Break Down Complex Problems: For complex percentage problems, break them down into smaller, more manageable steps.
-
Check Your Work: Always check your answers to ensure accuracy. Use different methods to verify your results.
Conclusion
Understanding percentages is a valuable skill with broad applications. By mastering the basic formula and different calculation methods, you'll be well-equipped to tackle various percentage problems effectively in academic settings, professional endeavors, and everyday life. Remember to practice consistently, understand the underlying concepts, and use different techniques to improve your accuracy and efficiency. The seemingly simple question, "What percentage of 30 is 27?" serves as a gateway to a deeper understanding of a fundamental mathematical concept with far-reaching implications.
Latest Posts
Latest Posts
-
The Mechanical Advantage Of The Wheel And Belt Assembly
May 14, 2025
-
80 Kilometers Equals How Many Miles
May 14, 2025
-
6500 A Month Is How Much An Hour
May 14, 2025
-
36 Out Of 60 As A Grade
May 14, 2025
-
How Many Drapery Panels Do I Need
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 30 Is 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.