Whats 4 To The Power Of 2
Treneri
May 12, 2025 · 6 min read
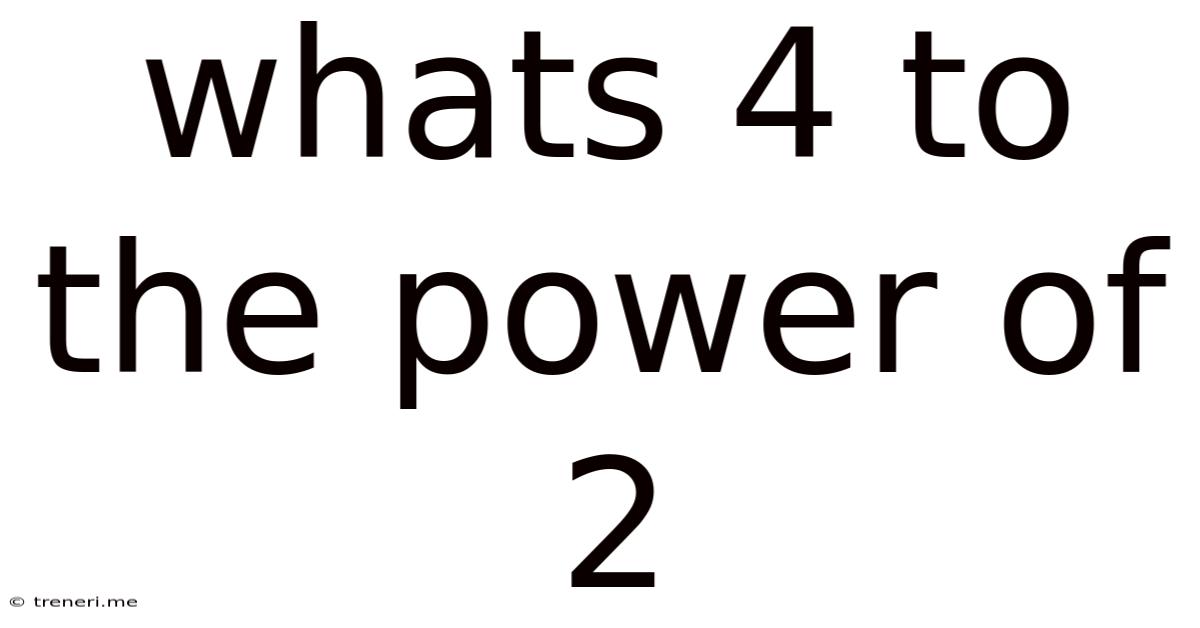
Table of Contents
What's 4 to the Power of 2? A Deep Dive into Exponents and Their Applications
What's 4 to the power of 2? The answer, simply put, is 16. But this seemingly straightforward mathematical problem opens the door to a fascinating exploration of exponents, their properties, real-world applications, and their significance in various fields, from basic arithmetic to advanced calculus and computer science. This article will delve into the concept of exponentiation, exploring its nuances and practical relevance in detail.
Understanding Exponents: A Foundation
Before we delve into the specifics of 4 to the power of 2, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression b<sup>n</sup>, 'b' represents the base and 'n' represents the exponent. This means we multiply 'b' by itself 'n' times.
For example:
- 2<sup>3</sup> = 2 x 2 x 2 = 8 (2 is the base, 3 is the exponent; 2 is multiplied by itself three times.)
- 5<sup>2</sup> = 5 x 5 = 25 (5 is the base, 2 is the exponent; 5 is multiplied by itself two times.)
- 10<sup>4</sup> = 10 x 10 x 10 x 10 = 10,000 (10 is the base, 4 is the exponent; 10 is multiplied by itself four times.)
This brings us back to our original question: What's 4 to the power of 2? This is expressed as 4<sup>2</sup>, which means 4 multiplied by itself two times: 4 x 4 = 16.
Beyond the Basics: Properties of Exponents
The concept of exponents extends far beyond simple calculations like 4<sup>2</sup>. Understanding the properties of exponents is crucial for solving more complex mathematical problems. These properties include:
1. Product of Powers:
When multiplying two numbers with the same base, you add the exponents: b<sup>m</sup> * b<sup>n</sup> = b<sup>(m+n)</sup>
For example: 2<sup>3</sup> x 2<sup>2</sup> = 2<sup>(3+2)</sup> = 2<sup>5</sup> = 32
2. Quotient of Powers:
When dividing two numbers with the same base, you subtract the exponents: b<sup>m</sup> / b<sup>n</sup> = b<sup>(m-n)</sup>
For example: 5<sup>4</sup> / 5<sup>2</sup> = 5<sup>(4-2)</sup> = 5<sup>2</sup> = 25
3. Power of a Power:
When raising a power to another power, you multiply the exponents: (b<sup>m</sup>)<sup>n</sup> = b<sup>(mn)</sup>*
For example: (3<sup>2</sup>)<sup>3</sup> = 3<sup>(2*3)</sup> = 3<sup>6</sup> = 729
4. Power of a Product:
When raising a product to a power, you raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>
For example: (2 x 3)<sup>2</sup> = 2<sup>2</sup> x 3<sup>2</sup> = 4 x 9 = 36
5. Power of a Quotient:
When raising a quotient to a power, you raise both the numerator and the denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>
For example: (4/2)<sup>3</sup> = 4<sup>3</sup> / 2<sup>3</sup> = 64 / 8 = 8
Understanding these properties is essential for manipulating and simplifying expressions involving exponents, laying the groundwork for more advanced mathematical concepts.
Real-World Applications of Exponents
The seemingly simple concept of exponents finds remarkable utility in a wide range of real-world applications:
1. Compound Interest:
Exponents play a crucial role in calculating compound interest. Compound interest is interest earned not only on the principal amount but also on accumulated interest. The formula for compound interest involves exponents, reflecting the exponential growth of the investment over time.
2. Population Growth:
Population growth often follows an exponential pattern. As populations increase, the rate of growth also increases, leading to exponential expansion. Mathematical models use exponential functions to predict future population sizes.
3. Radioactive Decay:
Radioactive substances decay at an exponential rate. The amount of remaining radioactive material decreases exponentially over time, a concept vital in fields like nuclear physics and medicine.
4. Computer Science:
Exponents are fundamental in computer science, particularly in algorithms and data structures. Big O notation, used to describe the efficiency of algorithms, often uses exponential functions to represent the growth of computation time as input size increases. Binary numbers, the foundation of digital computation, are intrinsically linked to powers of 2.
5. Physics and Engineering:
Exponential functions describe various physical phenomena, such as the decay of electrical charge in a capacitor, the growth and decay of oscillations in various systems, and the spread of heat. They are essential tools for solving problems in fields like mechanics, thermodynamics, and electromagnetism.
6. Economics and Finance:
Exponential functions are used to model economic growth, inflation rates, and stock market trends. They are instrumental in forecasting and risk management.
Expanding on 4 to the Power of 2: Further Exploration
While 4<sup>2</sup> = 16 is a straightforward calculation, it serves as a springboard for more in-depth exploration.
-
Square Roots: The square root of a number is a value that, when multiplied by itself, equals the original number. Therefore, the square root of 16 (√16) is 4, demonstrating the inverse relationship between squaring a number and finding its square root.
-
Higher Powers: We can extend this beyond the square. 4<sup>3</sup> (4 cubed) is 4 x 4 x 4 = 64. 4<sup>4</sup> is 4 x 4 x 4 x 4 = 256, and so on. This highlights the rapid growth of exponential functions as the exponent increases.
-
Negative Exponents: Exponents can also be negative. 4<sup>-2</sup> means 1/(4<sup>2</sup>) = 1/16. This introduces the concept of reciprocals and further expands the capabilities of exponential notation.
-
Fractional Exponents: Fractional exponents represent roots. For example, 4<sup>1/2</sup> is the square root of 4, which is 2. 4<sup>1/3</sup> is the cube root of 4, approximately 1.587. This opens up the concept of rational exponents and their relationship to roots.
Conclusion: The Significance of 4 to the Power of 2 and Beyond
The seemingly simple question, "What's 4 to the power of 2?" leads us on a journey through the fascinating world of exponents. It highlights their fundamental role in mathematics, their diverse applications across various disciplines, and their importance in understanding and modeling complex phenomena. From basic arithmetic to advanced scientific modeling, the concept of exponentiation serves as a cornerstone of mathematical understanding and problem-solving, enabling us to tackle intricate challenges across numerous fields. Mastering the concepts of exponents unlocks a deeper understanding of the world around us and empowers us to solve problems more effectively. The seemingly simple answer of 16 represents a gateway to a vast and powerful mathematical toolset.
Latest Posts
Latest Posts
-
How Much Is 700ml In Cups
May 12, 2025
-
What Is 4 Of 400 000
May 12, 2025
-
How To Calculate Velocity From Flow Rate
May 12, 2025
-
How Many Ounces Is 20 Cups
May 12, 2025
-
Can You Will Lottery Annuity Payments
May 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 4 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.